Question: You must write a report including your findings, all relevant information and computations, and provide evidence. For this project, you must download monthly historical data






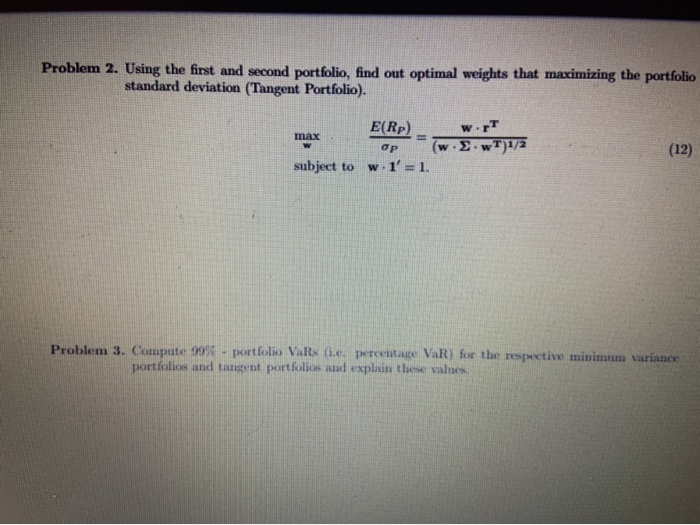


You must write a report including your findings, all relevant information and computations, and provide evidence. For this project, you must download monthly historical data from Jan. 2001 to Dec. 2019. Problem 1. Investigate important economic risk events since the year of 2000 and summarize them. Problem 2. TED spread is defined as the difference between 3 month LIBOR (loan) rate - 3 month T-bill rate." Compute monthly TED spreads from Jan. 2000 to Dec. 2019 and plot the TED spreads over time. Problem 3. Let us define a credit spread as the difference between US coporate bond yields and 10 year Treasury rate. For this exercise, use Bank of America Merrill Lynch US Corporate AAA Effective Yield as a corporate bond rate and 10-Year Treasury Constant Maturity Rate as Treasury rate." Compute monthly credit spreads from Jan. 2000 to Dec. 2019 and plot the credit spreads. Problem 4. In practice, a term spread is defined as 10 year Treasury rate mins 1 year Treasury rate. Calculate monthly term spreads from Jan. 2000 to Dec. 2019 and plot the term spreads. Problem 5. Examine time series plots from problem 2. 3, and 4 and suggest your findings. Suggest your findings on how these indicators responded against systemic shocks that you answered in problem 1. Problem 6. Examine yield curve shapes using daily yield curve rates provided by U.S. department of treasury a) Report treasure yield rates (1 month 3 month, 6 month, 1 year. 2 year. 3 year, 5 year, 7 nr. 10 year. 20 year. 30 year on Jan. 02. 2014. Jan. 02. 2015. Jan. 01, 2016. Jan. 03. 2017 Jan. 02. 2015. Jan. 02. 2019, and Jan. 02. 2020, b) Compute auch term pred for even term structures e) Ploten viele curves that show the relation between vields and maturities Prowide your findings thoroughly from bande), Problem 7. Compute montily S&P 500 index returns To calculate monthly returns using SX500 index price. You need to forma where it time in the refer to ontli: Saldes price at time. For example if you would like to computer Problem 5. Examine time series plots from problem 2, 3, and 4 and suggest your findings. Suggest your findinge on how these indicators responded against systemie shocks that you answered in problem 1. Problem 6. Examine yield curve shapes using daily yield curve rates provided by U.S. department of treasury a) Report treasure yield rates (1 month, 3 month, 6 month, 1 year, 2 year, 3 year, 5 year, 7 year, 10 year, 20 year, 30 year) on Jan. 02, 2014, Jan. 02, 2015, Jan. 04, 2016, Jan. 03, 2017, Jan. 02, 2018. Jan. 02, 2019, and Jan. 02, 2020. b) Compute each term spreads for seven term structures. e) Plot seven yield curves that show the relation between yields and maturities. d) Provide your findings thoroughly from b) and e). Problem 7. Compute monthly S&P 500 index returns. To calculate monthly returns using S&500 index price, you need to use formula as R A where I represents time (In our case, t refers to month: P represents the S&P index price at time t. For example, if you would like to compute a return on Feb. 2000, you may be able to specify an equation as R.,2000 = PP Problem 8. Using monthly returns that you obtained from the previous problem, compute monthly cu- mulative returns. To compute monthly cumulative returns, use the formula as CR, = R + DR., where CR, represents a cumulative return at time t. Problem 9. Plot monthly cumulative returns and examine how cumulative return series are affected by economic crisis. Also indicate bear or bull stages in the US stock market since the year of 2000. TED spread = math kan rate : 3 month T-bill rate Bof Merrill Lynch US Corporate AAA Effective Yield10-Year Treasury Constant Maturity Rate 10-Year Treasury Constant Maturity Rate Year Tiwary Constant Maturity Rate https www.try/ourcester/lata chart center/interest-rutes pages/textView.aspx?data=yeld Part 2 Portfolio Return and Risk Instruction: You are a portfolio investment analyst at Goldman Sachs. Your investment unit manages two equity portfolios - one portfolio, named P1, consists of two stock assets (Apple (AAPL) and Microsoft(Ticker: MSFT)) and the other portfolio, named P2, consists of five stocks (Disney(Ticker:DIS), Boeing(Ticker:BA), Amazon(Ticker:AMZN), Tesla(Ticker:TSLA), Netflix (Ticker:NFLX)). Now you are asked to compute two portfolio returns and risk measures. To do this, first download monthly stock prices from Dec 2009 to Dec. 2019 from Yahoo! Finance and compute monthly stock returns from Jan. 2010 to Dec. 2019.7 Problem 1. Compute the respective average, standard deviation, and covariance of monthly stock returns. Problem 2. Make two covariance matrices using two portfolio components. Note that you have to make a completed form of a matrix as below." SP: AAPL MSFT = OMSFT AAPL oiSFT = OMSFT.MSFT T:44P2) OMSFT.AAPL - CAAPL.MSFT (1) DISBA obis IBADIS AMZN.DIS ALSADES ONFLX DTS AMZN.BA OLSABA ODIS AMZN OBA AMZN OXMZN OTLSA.AMZN ONFLX.AMZN DISTLSA OBATLSA CAMZN.TLSA OTSA ONFLX TLSA DISNFLX OBANELX GAMZN.NFLX OTLSA, NFLX OF VELX (2) ONFLXIA Problem 3. Using the obtained statistics from problem 1. calculate an equal weighted portfolio return and portfolio variance for the first portfolio sing the below equations. Problem 3. Using the obtained statistics from problem 1, calculate an equal weighted portfolio return and portfolio variance for the first portfolio using the below equations. E(Rp.) = WAAPLTAAPL + WMSFTTMSFT (3) o} = oAPLOZAPL + wissFT SET + 2WAAPLUMSETO AAPLMSFT (4) Problem 4. Using the obtained statistics from problem 1, calculate an equal weighted portfolio return and portfolio variance for the second portfolio using the below equations. E(Rp) upsidis + BATBA + AMZNAMZN + TLSAFTLSA + INFLXNFLX (5) (6) os bobis + wc + mano man + wfisnoresa + w FuxoXFLX + 2wISDADIS. DA + PUDISHAMENDIS AMZN + 2uDISWT.SADISTUSA 2DISUNFLXODISNFLX + 2BAWANZNOBA AMZN + 2 BATLSA BATLSA 2DAUNFLXONANFLX + 20 MINUTESADAMENTLSA +2WMZNWNFLX AMZN.NFLX + 2TLSA NFLX TLSANFEX TR = where Represents a stock return attimet Asteck price at USTDEV Pin Excel STDEV S. Note that the formula for standard deviated a sample given by a ML while the form and evention on a population in weaten an PU Data Analysis Loops to matrix Problem 5. Using a matrix multiplication (i.e. MMULT in Excel.), compute two portfolio returns and portfolio variances. 10 E(Rp) = w.ET (7) on = w..w" (8) Problem 6. With the first portfolio, create a table that shows the benefit of diversification using Data Table in Excel. (Note that the table shows portfolio returns and portfolio standard deviation with respect to scenarios of weights on AAPL.) Problem 7. Using the table obtained from problem 6. Plot expected returns against portfolio risk (standard deviations) displaying efficient portfolios. Problem 8. Compute 99%-VaR and ES for the first and second portfolio components and explain these values. VaR(99%) = E(Rp) Zrap = E(Rp) +(99%)op (9) ES(99%) = E(Rp) - op 01 (1 -0.99) (10) 10.99 where of) is the normal density function. p ) is the inverse cumulative normal density function Note for Excel: Part 3 Minimum Variance and Tangent Portfolios Instruction: You have two customers that have different tastes of risk. The first customer is a risk averter who find the way of minimizing investment risk. The other customer is a kind of person who taking affordable risk that makes a risk adjusted return. Your boss asks you to find optimal weights of investments satisfying their risk-preferences. Problem 1. Using the first portfolio, find out optimal weights that minimizes the portfolio standard devi- ation (Minimum Variance Portfolio). min o=w. WT subject to w.."= E(Rp) (11) w.1' = 1. Problem 2. Using the first and second portfolio find out optimal weights that maximizing the portfolio stanlard deviation (Tangent Portfolio) ERP w FEN (12 ww12 w 11 subject to Problem 2. Using the first and second portfolio, find out optimal weights that maximizing the portfolio standard deviation (Tangent Portfolio). max E(Rp) OP subject to w. 1' = 1. WT w...wT)1/2 12) Problem 3. Compute 99% - portfolio VaRs (ie. percentage VaR) for the respective minimum variance portfolios and tangent portfolios and explain these values Part 4 Portfolio Evaluations and Systemic Risk Instruction: From the previous parts, you have created three portfolios with two stocks (equal weighted portfolio, minimum-variance portfolio, tangent portfolio). Now you are about to evaluating the performance of three portfolios. Problem 1. Download monthly stock prices for the period from Dec. 2019 to May 2020 using Yahoo! Finance and calculate monthly stock returns from Jan.2020 to May 2020. Problem 2. Using the obtained weights (equal weights and two sets of optimal weights) from part 1 and part 2. compute three monthly portfolio returns for each portfolio (P1 and P2) over the period from Jan.2020 to May 2020. Let denote EWP as an equal weighted portfolio, MVP as an minimum variance portfolio, and TP as a tangent portfolio Problem 3. Compute the respective averages, and standard deviations for EWP, MVP, TP based P1, Problem 4. Compute the respective averages, and standard deviations for EWP, MVP. TP bed P2. Problem 5. Compute the respective Sharpe Ratio SR) for the six portfolios using the below tation Problem 5. Compute the respective Sharpe Ratio (SR) for the six portfolios using the below equation. E(Rp) SR= (13) op Problem 6. Generate three cumulative returns and plot three cumulative returns based on Pl. Problem 7. Generate three cumulative returns and plot three cumulative returns based on P2. Problem 8. Let us examine the validity of 99%-VaR and ES. (a) How many monthly equal weighted portfolio returns are beyond 99% VaR and ES from Problem 8 in Part 1. (b) How many monthly minimum variance portfolio returns are beyond 99% VaR and ES from Problem 3 in Part 2 (e) How many monthly tangent portfolio returns are beyond 99% VaR and ES from Problem 3 in Part 2 Problem 9. Interpret all the results from problem 3 to problem 7. Also suggest your findings and your opinion about each portfolio performance during the period between Jan, 2020 to May 2020 You must write a report including your findings, all relevant information and computations, and provide evidence. For this project, you must download monthly historical data from Jan. 2001 to Dec. 2019. Problem 1. Investigate important economic risk events since the year of 2000 and summarize them. Problem 2. TED spread is defined as the difference between 3 month LIBOR (loan) rate - 3 month T-bill rate." Compute monthly TED spreads from Jan. 2000 to Dec. 2019 and plot the TED spreads over time. Problem 3. Let us define a credit spread as the difference between US coporate bond yields and 10 year Treasury rate. For this exercise, use Bank of America Merrill Lynch US Corporate AAA Effective Yield as a corporate bond rate and 10-Year Treasury Constant Maturity Rate as Treasury rate." Compute monthly credit spreads from Jan. 2000 to Dec. 2019 and plot the credit spreads. Problem 4. In practice, a term spread is defined as 10 year Treasury rate mins 1 year Treasury rate. Calculate monthly term spreads from Jan. 2000 to Dec. 2019 and plot the term spreads. Problem 5. Examine time series plots from problem 2. 3, and 4 and suggest your findings. Suggest your findings on how these indicators responded against systemic shocks that you answered in problem 1. Problem 6. Examine yield curve shapes using daily yield curve rates provided by U.S. department of treasury a) Report treasure yield rates (1 month 3 month, 6 month, 1 year. 2 year. 3 year, 5 year, 7 nr. 10 year. 20 year. 30 year on Jan. 02. 2014. Jan. 02. 2015. Jan. 01, 2016. Jan. 03. 2017 Jan. 02. 2015. Jan. 02. 2019, and Jan. 02. 2020, b) Compute auch term pred for even term structures e) Ploten viele curves that show the relation between vields and maturities Prowide your findings thoroughly from bande), Problem 7. Compute montily S&P 500 index returns To calculate monthly returns using SX500 index price. You need to forma where it time in the refer to ontli: Saldes price at time. For example if you would like to computer Problem 5. Examine time series plots from problem 2, 3, and 4 and suggest your findings. Suggest your findinge on how these indicators responded against systemie shocks that you answered in problem 1. Problem 6. Examine yield curve shapes using daily yield curve rates provided by U.S. department of treasury a) Report treasure yield rates (1 month, 3 month, 6 month, 1 year, 2 year, 3 year, 5 year, 7 year, 10 year, 20 year, 30 year) on Jan. 02, 2014, Jan. 02, 2015, Jan. 04, 2016, Jan. 03, 2017, Jan. 02, 2018. Jan. 02, 2019, and Jan. 02, 2020. b) Compute each term spreads for seven term structures. e) Plot seven yield curves that show the relation between yields and maturities. d) Provide your findings thoroughly from b) and e). Problem 7. Compute monthly S&P 500 index returns. To calculate monthly returns using S&500 index price, you need to use formula as R A where I represents time (In our case, t refers to month: P represents the S&P index price at time t. For example, if you would like to compute a return on Feb. 2000, you may be able to specify an equation as R.,2000 = PP Problem 8. Using monthly returns that you obtained from the previous problem, compute monthly cu- mulative returns. To compute monthly cumulative returns, use the formula as CR, = R + DR., where CR, represents a cumulative return at time t. Problem 9. Plot monthly cumulative returns and examine how cumulative return series are affected by economic crisis. Also indicate bear or bull stages in the US stock market since the year of 2000. TED spread = math kan rate : 3 month T-bill rate Bof Merrill Lynch US Corporate AAA Effective Yield10-Year Treasury Constant Maturity Rate 10-Year Treasury Constant Maturity Rate Year Tiwary Constant Maturity Rate https www.try/ourcester/lata chart center/interest-rutes pages/textView.aspx?data=yeld Part 2 Portfolio Return and Risk Instruction: You are a portfolio investment analyst at Goldman Sachs. Your investment unit manages two equity portfolios - one portfolio, named P1, consists of two stock assets (Apple (AAPL) and Microsoft(Ticker: MSFT)) and the other portfolio, named P2, consists of five stocks (Disney(Ticker:DIS), Boeing(Ticker:BA), Amazon(Ticker:AMZN), Tesla(Ticker:TSLA), Netflix (Ticker:NFLX)). Now you are asked to compute two portfolio returns and risk measures. To do this, first download monthly stock prices from Dec 2009 to Dec. 2019 from Yahoo! Finance and compute monthly stock returns from Jan. 2010 to Dec. 2019.7 Problem 1. Compute the respective average, standard deviation, and covariance of monthly stock returns. Problem 2. Make two covariance matrices using two portfolio components. Note that you have to make a completed form of a matrix as below." SP: AAPL MSFT = OMSFT AAPL oiSFT = OMSFT.MSFT T:44P2) OMSFT.AAPL - CAAPL.MSFT (1) DISBA obis IBADIS AMZN.DIS ALSADES ONFLX DTS AMZN.BA OLSABA ODIS AMZN OBA AMZN OXMZN OTLSA.AMZN ONFLX.AMZN DISTLSA OBATLSA CAMZN.TLSA OTSA ONFLX TLSA DISNFLX OBANELX GAMZN.NFLX OTLSA, NFLX OF VELX (2) ONFLXIA Problem 3. Using the obtained statistics from problem 1. calculate an equal weighted portfolio return and portfolio variance for the first portfolio sing the below equations. Problem 3. Using the obtained statistics from problem 1, calculate an equal weighted portfolio return and portfolio variance for the first portfolio using the below equations. E(Rp.) = WAAPLTAAPL + WMSFTTMSFT (3) o} = oAPLOZAPL + wissFT SET + 2WAAPLUMSETO AAPLMSFT (4) Problem 4. Using the obtained statistics from problem 1, calculate an equal weighted portfolio return and portfolio variance for the second portfolio using the below equations. E(Rp) upsidis + BATBA + AMZNAMZN + TLSAFTLSA + INFLXNFLX (5) (6) os bobis + wc + mano man + wfisnoresa + w FuxoXFLX + 2wISDADIS. DA + PUDISHAMENDIS AMZN + 2uDISWT.SADISTUSA 2DISUNFLXODISNFLX + 2BAWANZNOBA AMZN + 2 BATLSA BATLSA 2DAUNFLXONANFLX + 20 MINUTESADAMENTLSA +2WMZNWNFLX AMZN.NFLX + 2TLSA NFLX TLSANFEX TR = where Represents a stock return attimet Asteck price at USTDEV Pin Excel STDEV S. Note that the formula for standard deviated a sample given by a ML while the form and evention on a population in weaten an PU Data Analysis Loops to matrix Problem 5. Using a matrix multiplication (i.e. MMULT in Excel.), compute two portfolio returns and portfolio variances. 10 E(Rp) = w.ET (7) on = w..w" (8) Problem 6. With the first portfolio, create a table that shows the benefit of diversification using Data Table in Excel. (Note that the table shows portfolio returns and portfolio standard deviation with respect to scenarios of weights on AAPL.) Problem 7. Using the table obtained from problem 6. Plot expected returns against portfolio risk (standard deviations) displaying efficient portfolios. Problem 8. Compute 99%-VaR and ES for the first and second portfolio components and explain these values. VaR(99%) = E(Rp) Zrap = E(Rp) +(99%)op (9) ES(99%) = E(Rp) - op 01 (1 -0.99) (10) 10.99 where of) is the normal density function. p ) is the inverse cumulative normal density function Note for Excel: Part 3 Minimum Variance and Tangent Portfolios Instruction: You have two customers that have different tastes of risk. The first customer is a risk averter who find the way of minimizing investment risk. The other customer is a kind of person who taking affordable risk that makes a risk adjusted return. Your boss asks you to find optimal weights of investments satisfying their risk-preferences. Problem 1. Using the first portfolio, find out optimal weights that minimizes the portfolio standard devi- ation (Minimum Variance Portfolio). min o=w. WT subject to w.."= E(Rp) (11) w.1' = 1. Problem 2. Using the first and second portfolio find out optimal weights that maximizing the portfolio stanlard deviation (Tangent Portfolio) ERP w FEN (12 ww12 w 11 subject to Problem 2. Using the first and second portfolio, find out optimal weights that maximizing the portfolio standard deviation (Tangent Portfolio). max E(Rp) OP subject to w. 1' = 1. WT w...wT)1/2 12) Problem 3. Compute 99% - portfolio VaRs (ie. percentage VaR) for the respective minimum variance portfolios and tangent portfolios and explain these values Part 4 Portfolio Evaluations and Systemic Risk Instruction: From the previous parts, you have created three portfolios with two stocks (equal weighted portfolio, minimum-variance portfolio, tangent portfolio). Now you are about to evaluating the performance of three portfolios. Problem 1. Download monthly stock prices for the period from Dec. 2019 to May 2020 using Yahoo! Finance and calculate monthly stock returns from Jan.2020 to May 2020. Problem 2. Using the obtained weights (equal weights and two sets of optimal weights) from part 1 and part 2. compute three monthly portfolio returns for each portfolio (P1 and P2) over the period from Jan.2020 to May 2020. Let denote EWP as an equal weighted portfolio, MVP as an minimum variance portfolio, and TP as a tangent portfolio Problem 3. Compute the respective averages, and standard deviations for EWP, MVP, TP based P1, Problem 4. Compute the respective averages, and standard deviations for EWP, MVP. TP bed P2. Problem 5. Compute the respective Sharpe Ratio SR) for the six portfolios using the below tation Problem 5. Compute the respective Sharpe Ratio (SR) for the six portfolios using the below equation. E(Rp) SR= (13) op Problem 6. Generate three cumulative returns and plot three cumulative returns based on Pl. Problem 7. Generate three cumulative returns and plot three cumulative returns based on P2. Problem 8. Let us examine the validity of 99%-VaR and ES. (a) How many monthly equal weighted portfolio returns are beyond 99% VaR and ES from Problem 8 in Part 1. (b) How many monthly minimum variance portfolio returns are beyond 99% VaR and ES from Problem 3 in Part 2 (e) How many monthly tangent portfolio returns are beyond 99% VaR and ES from Problem 3 in Part 2 Problem 9. Interpret all the results from problem 3 to problem 7. Also suggest your findings and your opinion about each portfolio performance during the period between Jan, 2020 to May 2020
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


