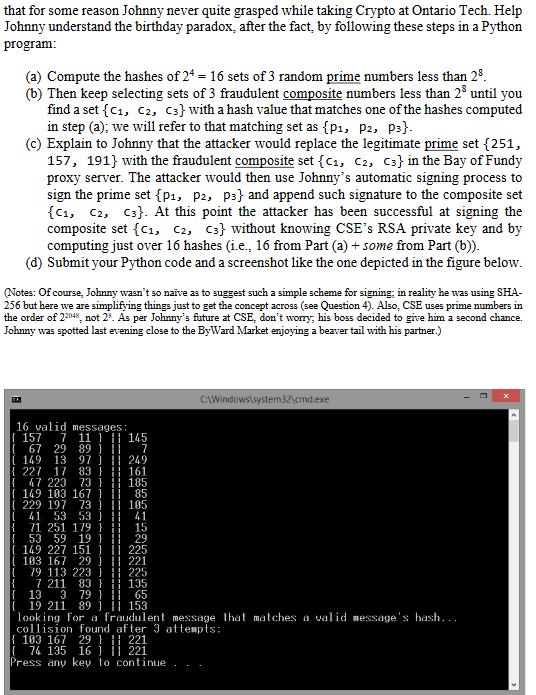
You need to generate the hashes of 16 sets of 3 random prime numbers less than 256. Then keep computing the hash value of different sets of 3 composite numbers less than 256 until you find a set that matches one of the 16 hash values of the random prime numbers. The formal definition of a "set" is "an unordered collection of distinct objects". This means a "set" has no repeated elements, and the order in which they are written doesn't matter. Therefore, no, there can't be repeated elements, and set {x, y, z} is the same as set {z, x, y}.

Johnny, an Ontario Tech graduate recently got a job at CSE in Ottawa. As part of a pilot project, every month CSE announces a list of 3 prime numbers (all less than 29) in proxy repositories which automatically sign the 3 numbers for Navy bases across the Country to fetch them. These numbers become part of public keys so confidentiality is not required, only signature. In his very first day at work, Johnny volunteers to take charge of the automatic signature generation in the Bay of Fundy proxy (as, according to Johnny, it was close enough to his native St. John's). He decided to sign the 3 numbers using a hash value consisting of the bitwise XOR amongst the bit representation of these 3 numbers and then encrypting the hash value using CSE's private RSA key. Further, he made sure his automatic process only signed the numbers if all of the 3 numbers were prime (i.e., if at least one of the 3 numbers were composite the process would refuse to sign). Last month's numbers were {251, 157, 191}. Johnny's program computed the hash to be 217 (because 251 XOR 157 XOR 191 = 217) which then was encrypted with RSA and appended to the set of numbers as signature. Shortly after, CSE suspected a probable compromise of the Bay of Fundy proxy since the Nova Scotia Navy Base ended up using composite numbers in their crypto operations causing serious disruptions in the pilot project! During his debrief, Johnny claimed that to forge the signature with probability , 28 an attacker would need to compute the hash values of =2' =128 sets of 3 random composite numbers, not to mention that the attacker would require to break RSA. But his boss, an experienced cryptographer advises that Johnny's claims were overly optimistic, saying that the attacker could forge a signature with probability greater than % by computing the hashes of only 2*2 = 2* = 16 (not 128) sets of 3 random composite numbers, and that the attacker wouldn't even have to break RSA at all. Johnny was speechless! In her explanation, Johnny's boss alluded to the birthday paradox, a concept