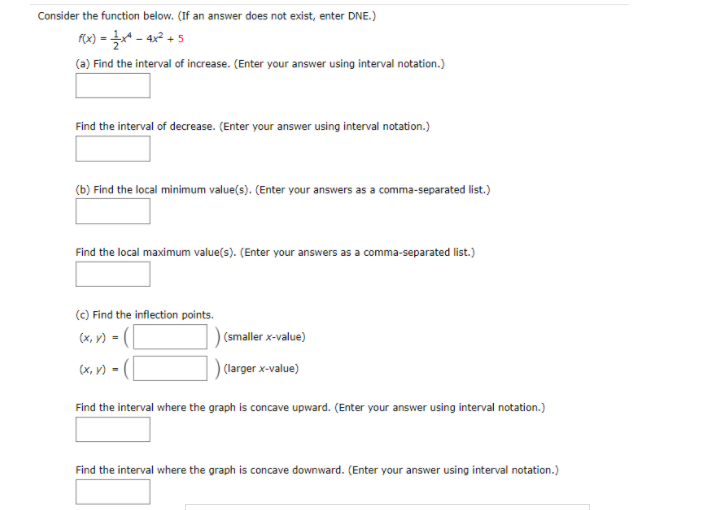
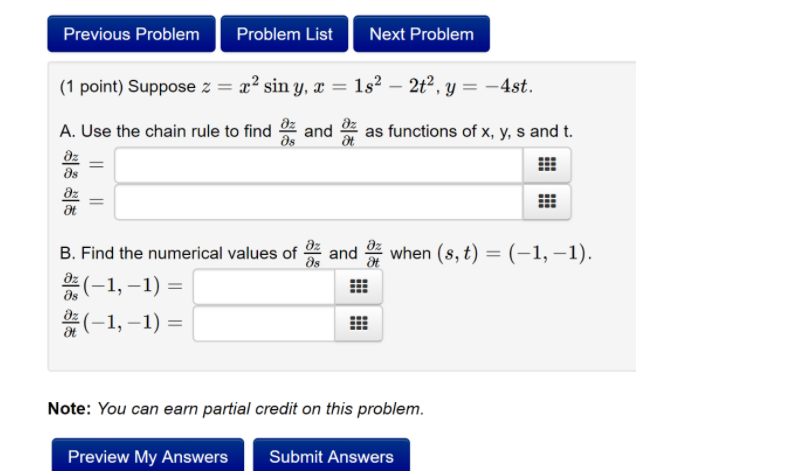
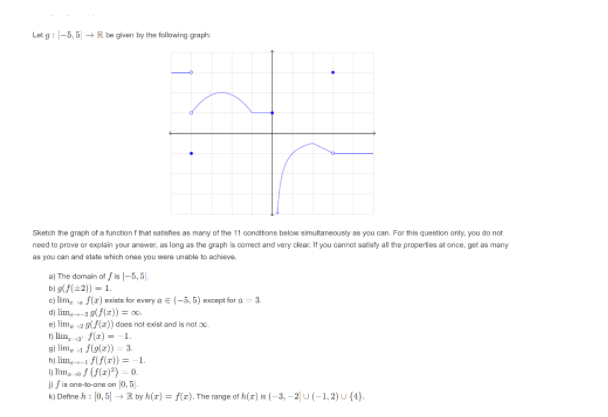
zd 1

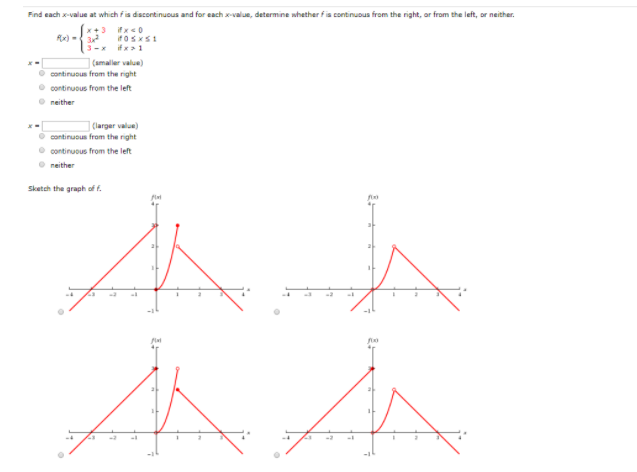
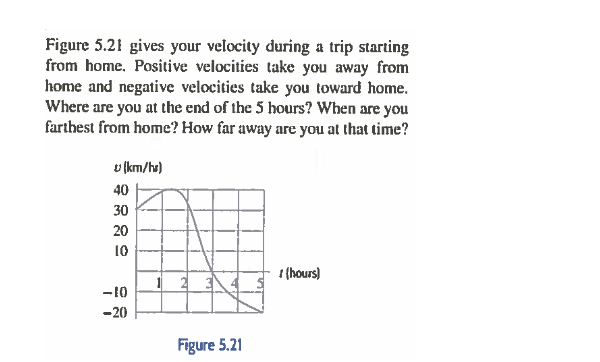
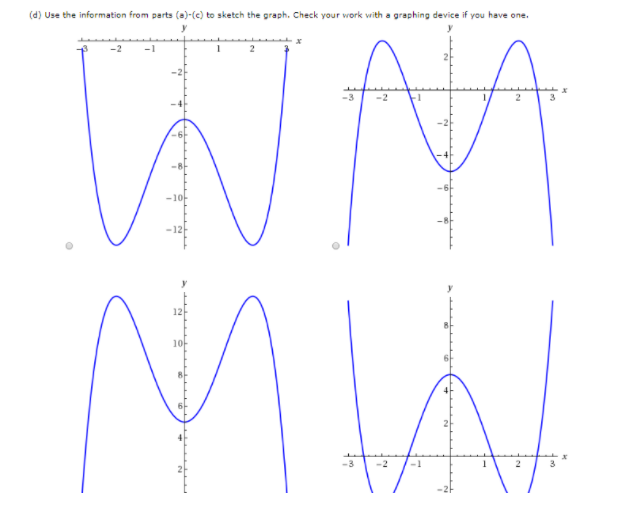
Find each x-value at which f is discontinuous and for each x-value, determine whether fis continuous from the right, or from the left, or neither. 3 - 2 (smaller value) 0 continuous from the right 0 continuous from the left O neither (larger value) 0 continuous from the right 0 continuous from the left O neither Sketch the graph of F.25. Roger runs a marathon. His friend Jel't'rides behind him on a bicycle and eloelts his speed CW\"? 15 minutes. Roger starts out strong. but after an hour and a half he is so exhausted that he has to stop. lelf's dale follow: 11... sincemniminl \"IRENE- an in) assuming that Roger's speed is never increasing. give upper and lower estimates for the distance Rogerraa during the rst halt\" hour. {it} Give upper and lower estimates for the disteaee Roger ran in total during the entire hour and a half. It] How often would Jeli' have needed to measure Roger's speed in order to find lower and upper es. timates within {LI mile of the actual distance he ran\"? Figure 5.21 gives your velocity during a trip starting from home. Positive velocities take you away from home and negative velocities take you toward home. Where are you at the end of the 5 hours? When are you farthest from home? How far away are you at that time? u (km/h) 40 30 I (hours) -10 -20 Figure 5.21Consider the equation below. (If an answer does not exist, enter DNE.) f(x) - x In(x) (a) Find the interval on which f is increasing. (Enter your answer using interval notation.) Find the interval on which f is decreasing. (Enter your answer using interval notation.) (b) Find the local minimum and maximum values of f. local minimum value local maximum value (c) Find the inflection point. (x, V) = ( Find the interval on which fis concave up. (Enter your answer using interval notation.) Find the interval on which fis concave down. (Enter your answer using interval notation.)(d) Use the information from parts (a)-(c) to sketch the graph. Check your work with a graphing device if you have one. -2 ULX -3 -2 L 2 -26 -4 -6 12 10- 4- 2 -21Consider the function below. (If an answer does not exist, enter DNE.) ((x) = 1x - 4x2+ 5 (a) Find the interval of increase. (Enter your answer using interval notation.) Find the interval of decrease. (Enter your answer using interval notation.) (b) Find the local minimum value(s). (Enter your answers as a comma-separated list.) Find the local maximum value(s). (Enter your answers as a comma-separated list.) (c) Find the inflection points. (x, V ) = (smaller x-value) (x, V) = (larger x-value) Find the interval where the graph is concave upward. (Enter your answer using interval notation.) Find the interval where the graph is concave downward. (Enter your answer using interval notation.)Previous Problem Problem List Next Problem (1 point) Suppose z = a siny, x = 182 - 2t', y = -4st. A. Use the chain rule to find % and as functions of x, y, s and t. 8z B. Find the numerical values of and when (s, t) = (-1, -1). Oz (-1, -1) = az at (-1, -1) Note: You can earn partial credit on this problem. Preview My Answers Submit Answers3. Evaluate the following integrals. You may have to use algebra, educated guess-and-check, and/or recognize an integrand as the result of a product or quotient calculation. Note, when using FTOC part I, you do not need to check that the hypothesis is true before using the consequent; This is the only theorem where we will be allowed to do this 'omission of checking hypothesis'. (b) / cos ' (x + 1)de (d) (20 - 1)(u' + u)?du (e) sec'(t)elt (g) Let a,bERt, / a (1+6 " )dx (h) 'sin(z) cos(z) sin'(r)dr (1) 2rIn(x) - r (In(r)) ( k) de (2r + 1)1Let g : |-5,5] + R be given by the following graph: Sketch the graph of a function f that satisfies as many of the 11 conditions below simultaneously as you can. For this question only. you do not need to prove or explain your answer, as long as the graph is comect and very clear. If you cannot satisfy all the properties at once. get as many an you can and state which ones you were unable to achieve. a] The domain of / Is |-5, 5]. big(/(3)] - 1. c) lim, . /(x) exists for every a = (-5. 5) except for a = 3. di lim,-." (/(=)) = 0 el lim. . s( /(a)) does not exist and is not oo plim, ' /(2) = -1. pi lim, " flo(e)) = 3. hi lim,-+-1 f(/(r)) = -1. DEma / (/(=] ) =0. D / in one-to-one on (0, 5]. kj Define h : [0, 5) -+ 3 by A(x) = /(x). The range of h(x] is (-3, -2 0 (-1,2) 0 14)