Consider the nonlinear regression model fit to the data in Problem 12.11. Find the bootstrap standard errors for the regression coefficients \(\hat{\theta}_{1}, \hat{\theta}_{2}\), and \(\hat{\theta}_{3}\) using \(m=1000\) bootstrap samples. Based on the results you obtain, comment on how the asymptotic theory seems to apply to this problem.

Data From Problem 12.11

The data below represent the fraction of active chlorine in a chemical product as a function of time after manufacturing.

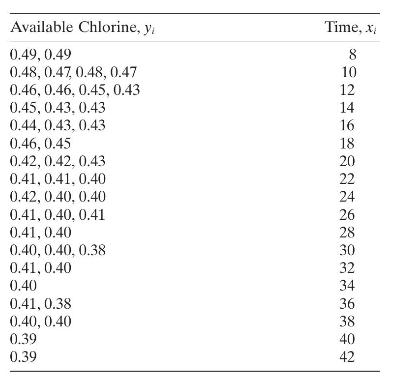
a. Construct a scatterplot of the data.
b. Fit the Mitcherlich law (see Problem 12.10) to these data. Discuss how you obtained the starting values.

Data From Problem 12.10

12.10 Consider the model
\[
y=\theta_{1}-\theta_{2} e^{-\theta_{3} x}+\varepsilon
\]
This is called the Mitcherlich equation, and it is often used in chemical engineering. For example, \(y\) may be yield and \(x\) may be reaction time.

c. Test for significance of regression.
d. Find approximate \(95 \%\) confidence intervals on the parameters \(\theta_{1}, \theta_{2}\), and \(\theta_{3}\). Is there evidence to support the claim that all three parameters are different from zero?
e. Analyze the residuals and comment on model adequacy.

Transcribed Image Text:

Available Chlorine, y 0.49, 0.49 0.48, 0.47, 0.48, 0.47 Time, x 8 10 0.46, 0.46, 0.45, 0.43 12 0.45, 0.43, 0.43 14 0.44, 0.43, 0.43 16 0.46, 0.45 18 0.42, 0.42, 0.43 20 0.41, 0.41, 0.40 22 0.42, 0.40, 0.40 24 0.41, 0.40, 0.41 0.41, 0.40 0.40, 0.40, 0.38 26 28 0.41, 0.40 0.40 0.41, 0.38 0.40, 0.40 0.39 30 32 34 36 38 40 0.39 42