Consider the simple regression model fit to the National Football League team performance data in Problem 2.1.

Data From Problem 2.1

Table B. 1 gives data concerning the performance of the 26 National Football League teams in 1976. It is suspected that the number of yards gained rushing by opponents $\left(x_{8}\right)$ has an effect on the number of games won by a team $(y)$.

a. Construct a normal probability plot of the residuals. Does there seem to be any problem with the normality assumption?

b. Construct and interpret a plot of the residuals versus the predicted response.

c. Plot the residuals versus the team passing yardage, $x_{2}$. Does this plot indicate that the model will be improved by adding $x_{2}$ to the model?

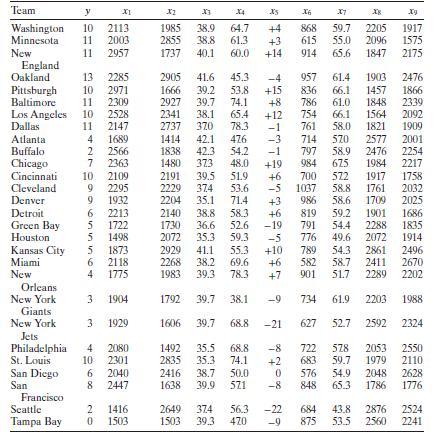
Transcribed Image Text:

Team y x1 32 33 X4 X5 X6 X7 xx Xy Washington 10 2113 1985 38.9 64.7 Minnesota 11 2003 2855 38.8 61.3 New 11 2957 1737 England 79 +4 868 59.7 2205 1917 +3 615 55.0 2096 1575 40.1 60.0 +14 914 65.6 1847 2175 Oakland 13 2285 2905 41.6 45.3 -4 957 61.4 1903 2476 Pittsburgh 10 2971 1666 39.2 53.8 +15 836 66.1 1457 1866 Baltimore 11 2309 2927 39.7 74.1 +8 786 61.0 1848 2339 Los Angeles 10 2528 2341 38.1 65.4 +121 754 66.1 1564 2092 Dallas 11 2147 2737 370 78.3 -1 761 58.0 1821 1909 Atlanta 4 1689 1414 42.1 476 -3 714 570 2577 2001 Buffalo 2 2566 1838 42.3 54.2 -1 797 58.9 2476 2254 Chicago 7 2363 1480 373 48.0 +19 984 675 1984 2217 Cincinnati 10 2109 2191 39.5 51.9 Cleveland 9 2295 2229 374 53.6 -5 Denver 9 1932 2204 35.1 71.4 Detroit 6 2213 2140 38.8 58.3 Green Bay 5 1722 1730 36.6 Houston 5 1498 2072 35.3 59.3 Kansas City 5 1873 2929 41.1 Miami 6 2118 2268 38.2 New 4 1775 1983 39.3 78.3 Orleans New York 3 1904 1792 39.7 38.1 Giants New York 3 1929 1606 39.7 68.8 Jets Philadelphia 4 2080 1492 35.5 68.8 St. Louis 10 2301 2835 35.3 74.1 San Diego San 6 2040 2416 38.7 50.0 8 2447 1638 39.9 521 Francisco Scattle Tampa Bay 20 1416 0 1503 2649 374 1503 56.3 39.3 470 - +6 700 572 1917 1758 1037 58.8 1761 2032 +3 986 58.6 1709 2025 +6 52.6 -19 791 819 59.2 54.4 1901 1686 2288 1835 -5. 776 49.6 2072 1914 55.3 +10 789 54.3 2861 2496 69.6 +6 582 58.7 +7 901 51.7 2411 2670 2289 2202 734 61.9 2203 1988 -21 627 52.7 2592 2324 -8 722 578 2053 2550 +2 683 59.7 1979 2110 0 576 54.9 2048 2628 -8 848 65.3 1786 1776 -22 684 43.8 2876 2524 -9 875 53.5 2560 2241