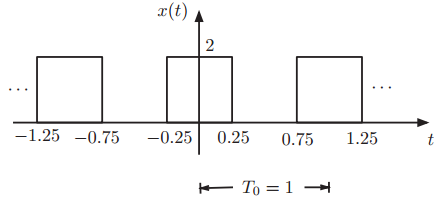
Consider the integral of the Fourier series of the pulse signal p(t) = x(t) 1 of period

Consider the integral of the Fourier series of the pulse signal p(t) = x(t) ˆ’1 of period T₀= 1, where x(t) is given in Figure 4.22.

(a) Given that an integral of p(t) is the area under the curve, find and plot the function

indicate the values of s(t) for t = 0, 0.25, 0.5, 0.75, and 1.

(b) Find the Fourier series of p(t) and s(t) and relate their Fourier series coefficients.

(c) Suppose you want to compute the integral

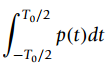
using the Fourier series of p(t). What is the integral equal to?

(d) You can also compute the integral from the plot of p(t)

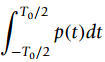
What is it? Does it coincide with the result obtained using the Fourier series? Explain

Figure 4.22:

Transcribed Image Text:

s(t) = t < 1 rTo/2 p(t)dt -To/2