In the following problems properties of the Laplace transform are used.

(a) Show that the Laplace transform of x(t) e^ˆ’at u(t)is X(s + a), where X(s) = L[x(t)] and then use it to find the Laplace transform of y(t) = cos(t) e^ˆ’2tu(t).

(b) A signal x₁(t) has as Laplace transform

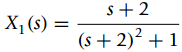
find poles and zeros of X₁ (s) and find x₁(t) as t †’ ˆž from the location of the poles.

(c) The signal z(t) = de^ˆ’t u(t)/dt,

i. Compute the derivative z(t)and then find its Laplace transform Z(s).

ii. Use the derivative property to find Z(s). Compare your result with the one obtained above.

Transcribed Image Text:

s+ 2 X, (s) = (s + 2) +1