Signals of finite time support have infinite support in the frequency domain, and a band-limited signal has infinite time support. A signal cannot have finite support in both domains.

(a) Consider the signals x(t) = e^ˆ’t2(the Gaussian function) and x₁(t) = u(t + 1) ˆ’ u(t ˆ’ 1). Use MATLAB to find their Fourier transform X(Ω), and X₁(Ω), and to compute the energy of the signals in Ω ­ˆˆ [ˆ’4, 4].

(b) The fact that a signal cannot be of finite support in both domains is expressed well by the uncertainty principlewhich says that

2ˆ†(t) ˆ†(Ω) ‰¥ 1

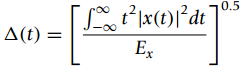
measures the duration of the signal for which the signal is significant in time, and

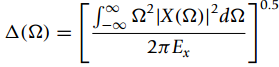
measures the frequency support for which the Fourier representation is significant. The energy of the signal is represented by Ex. Use MATLAB to compute ˆ†(t) and ˆ†(Ω) for the signals x(t) and x₁(t) and verify that the uncertainty principle is satisfied. Comment on the difference in results for the two signals; pay attention to the smoothness and the frequency content of the signals.

Transcribed Image Text:

[ oά 0.5 Δ( ) ψε 0.5 Δ (Ω)- UP (0)X υ 2πΕ