Three laws in the computation of sums are for any permutation p(k) of the set of integers
Question:
Three laws in the computation of sums are
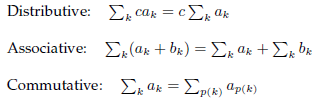
for any permutation p(k) of the set of integers k in the summation.
(a) Explain why the above rules make sense when computing sums. To do that consider
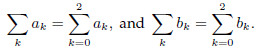
Let c be a constant, and choose any permutation of the values [0; 1; 2] for instance [2; 1; 0] or [1; 0; 2].
(b) The trick that Gauss played when he was a preschooler can be explained by using the above rules. Suppose you want to find the sum of the integers from 0 to 10; 000 (Gauss did it for integers between 0 and 100 but he was then just a little boy, and we can do better!). That is, we want to find S where
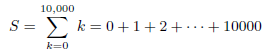
to do so consider
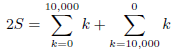
and apply the above rules to find then S. Come up with a MATLAB function of your own to do this sum.
(c) Find the sum of an arithmetic progression

for constants and , using the given three rules.
(d) Find out if MATLAB can do these sums symbolically, i.e., without having numerical values. Use the found symbolic function to calculate the sum in the previous item when α = β = 1 and N = 100.
Step by Step Answer:

Signals and Systems using MATLAB
ISBN: 978-0128142042
3rd edition
Authors: Luis Chaparro, Aydin Akan





