Consider the infinite series for the Madelung constant of the NaCl-type structure. Its convergence depends on how
Question:
Consider the infinite series for the Madelung constant of the NaCl-type structure. Its convergence depends on how the successive terms are chosen. As written in Equation (5.2), each successive shell contains ions of the same type (either cations or anions).
(a) Calculate the sum of this series for two shells, three shells, etc., up to the full seven shells listed in Equation (5.2). For each successive shell, determine the total number of cations and anions surrounding the central anion.
(b) What can you say about the convergence of this series after seven terms?
(c) Which of these successive sums is closest to the Madelung constant value of +1.7476? For which sum is the total charge of the cluster closest to zero?
(d) What can be done to achieve a more rapid convergence of this series?
Equation (5.2)
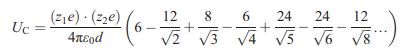
Step by Step Answer:

Solid State Materials Chemistry
ISBN: 9780521873253
1st Edition
Authors: Patrick M. Woodward, Pavel Karen, John S. O. Evans, Thomas Vogt





