Question: For couplings between spins, we can construct four independent Hermitian coupling matrices, Show explicitly, by calculating the characters for the C 2 and C 4

For couplings between spins, we can construct four independent Hermitian coupling matrices,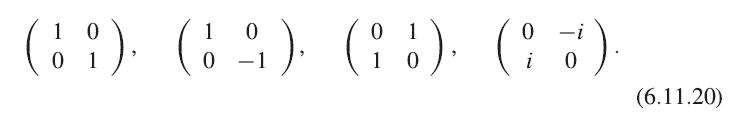 0 0 (1) 619) (15). (97). -1 0 i (6.11.20)

Show explicitly, by calculating the characters for the C₂ and C₄ rotations, that one of these matrices can act as the basis of a D⁺₀ representation of the full rotation symmetry group, and the other three can act as the basis functions for a D⁺₁ representation, that is, they transform as L_x, L_y, L_z. The rotation matrix acting on a spinor, for a rotation of angle θ around an axis n̂, is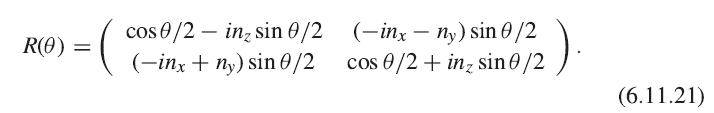

By the method of invariants, we can then multiply each by the magnetic field component that transforms the same way, to get the Hamiltonian for the effect of magnetic field on a particle with spin. Write down this full Hamiltonian. Note that spin, angular momentum, and magnetic field are all even under an inversion transformation I.

0 0 (1) 619) (15). (97). -1 0 i (6.11.20)

Step by Step Solution

★★★★★

3.60 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The characters of the full rotation group from Table 613 in the book are E C6 C4 C3 C2 D D C 1 3 A C ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Solid State Physics Essential Concepts Questions!

The Farmers American Bank of Leesburg is planning to install a new computerized accounts system. Bank management has determined the activities required to complete the project, the precedence...

The birth of the Internet in the 1990s led to the creation of a new industry of online retailers such as Amazon, Overstock.com, and PC Mall, Inc. Many of these companies often act as intermediaries...

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

According to the reading by Turner, why is film considered a type of language? 3 FILM LANGUAGES The title of this chapter may require explanation. Film is not, of course, a language but it does...

Q1) Should Cameron have licensed McTaggart or continued to export? Q2) Was McTaggart a good choice for licensee? Q3) Was the royalty rate reasonable? Q4) What about the alternatives to licensing?...

4. If you were in the position of George Smith, what decision you would have taken for Top Gear? In the spring of 2013, George Smith had just come back from a trip to Scotland with a signed contract...

3 . Explain the possible alternatives to licensing for Top Gear? 4 . If you were in the position of George Smith, what decision you would have taken for Top Gear? In the spring of 2013, George Smith...

1 . What could have been the best option for Top Gear to take for its internationalization move, i.e., either exporting or licensing? Discuss your answer based on the advantages of exporting and...

Q4) What about the alternatives to licensing? Q11) Explain the TWO(2) ways how an unrelated diversification strategy can create value. Q12) (a) Discuss the motives for firms to pursure international...

A box of bananas weighing 40.0 N rests on a horizontal surface. The coefficient of static friction between the box and the surface is 0.40, and the coefficient of kinetic friction is 0.20. (a) If no...

Let F, G: R3 R3 and f : R3 R be differentiable. Prove the following analogues of the Sum and Product Rules for the "derivatives" curl and divergence. a) (F + G) = ( F) + ( G) b) (fF) = f( F)...

Lily Landscaping Inc is preparing its budget for the frrst quarter of 2 0 2 7 . The next step in the budgeting process is to prepare a cash receipts schedule and a cash payments schedule. To that...

28. If a non-critical activity has no free float, it implies that the start of one or more of its immediately succeeding activities is dependent on the completion time of this activity. Mark the...

We have seen that NaH is a strong base but a weak nucleophile. In contrast, lithium aluminum hydride (LAH) is a reagent that can serve as a source of nucleophilic hydride ion: In this case, LAH...

a) NaOH is a strong nucleophile and strong base. The substrate in this case is primary. Therefore, we expect S N 2 (giving the major product) and E2 (giving the minor product). b) NaSH is a strong...

Calculate w, q, H, and U for the process in which 1.75 mol of water undergoes the transition H 2 O(l, 373 K) H 2 O(g, 610.K) at 1 bar of pressure. The volume of liquid water at 373 K is 1.89 10 5 m...

ABC Treasures Limited purchased a piece of equipment on January 1, 2020 for $56,000. The equipment is expected to have a 4 year useful life and an $4,000 residual value. ABC has a December 31, 2020...

Descriptive Question and Answers 1. Define a simulation model. What is Monte Carlo simulation

Prepare the Production Department's flexible budget for the month. Prepare the Production Department's flexible budget performance report for March, Including both the spending and activity...