Question: Show that (4.2.13) is equal to (4.2.14) by substituting into (4.2.14) the definitions of a k and a k . You will need to

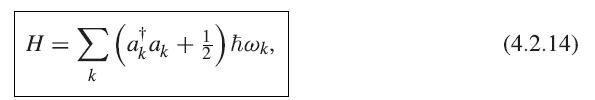
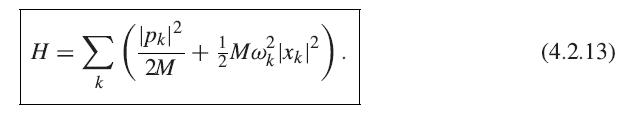
Show that (4.2.13) is equal to (4.2.14) by substituting into (4.2.14) the definitions of a_k and a^†_k. You will need to use the definitions of x_k and p_k in terms of x_n and p_n, and the relation [x_n, p_n_′ ] = ih̄δ_n,n_′. = (atak + 2 ) ha hok, k H = (4.2.14)

= (atak + 2 ) ha hok, k H = (4.2.14)

Step by Step Solution

★★★★★

3.48 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

and From Eq 414 and Eq 423 we have Mwk k Pk 1 N 1 V... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Solid State Physics Essential Concepts Questions!

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-4. Ivan and Irene paid the following in 2012 (all by check or can otherwise be...

A compare-exchange operation on two array elements A[i] and A[j], where i A[j] 2 exchange A[i] with A[j] After the compare-exchange operation,...

Please solve using the Excel Solver, if possible. The "Fair Election Districting" problem is much harder than the one we will solve, but it is representative. Let us assume we have identified 3...

Introduction to Competencies Competencies are probably most closely related to abilities. However, in our craft, Learning and Development, the term ability normally means either able to do or a...

1. Chapter 7 -- Problems 9, 12, 31, & 55. 2. Use the Excel data file in Canvas for Problems 12, 31, and 55. 3. Submit your work by the due date (TBA). No late submission nor redo assignment will be...

Chapter 25: Consumer Choice: Terms & Definitions Examples from Class & Mr. Han's Examples Concepts, Graphs, Tables Including (but not limited to) ... o Indifference Curves (IC) o Budget Constraints...

Intro to Python: Implementing the Sensor Dictionary and List, and Applying a Filter I'm supposed to implement a menu that runs the function below. This class is quite difficult for me despite it...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

A shareholder of Company B is concerned about the recent performance of the company. She has collected the following financial information. Year to 31 December 2019 2020 2021 Revenue in 'm 9.4 9.6...

On September 30, 2021, Ferguson Imports leased a warehouse. Terms of the lease require Ferguson to make 15 annual lease payments of $52,000 with the first payment due immediately. Accounting...

A bond's yield moves from 5 . 0 0 % to 6 . 0 0 % . The yield has increased by: A 1 point 1 basis point 1 0 0 basis points 1 , 0 0 0 basis points

4 What benefits and problems might having two chief executives present to developing and implementing a growth strategy?

Give an example of two systems that are in equilibrium with respect to only one of two state variables.

Aerobic cells metabolize glucose in the respiratory system. This reaction proceeds according to the overall reaction 6O 2 (g) + C 6 H 12 O 6 (s) 6CO 2 (g) + 6H 2 O(l) Calculate the volume of oxygen...

Using acetylene as your only source of carbon atoms, outline a synthesis for 3-hexyne.

Question 1 Arcade Corporation's balance sheet and income statement appear below: Income Statement Sales $723 Cost of goods sold 453 Gross margin 270 Selling and administrative expenses 163 Income...

Diego Company manufactures one product that is sold for $80 per unit in two geographic regionsthe East and West regions. The following information pertains to the company's first year of operations...

please help Apple Inc. CONSOLIDATED STATEMENTS OF SHAREHOLDERS' EQUITY (In millions) Years ended Total shareholders' equity, beginning balances Common stock and additional paid-in capital Beginning...