Suppose we have a ring with six identical atoms. This is a periodic sytem in one dimension, so the Bloch theorem applies. According to the LCAO approximation, discussed in Section 1.1.2, we write the wave function as a linear combination of the unperturbed atomic wave orbitals. This allows us to write a matrix for the eigenstates as follows: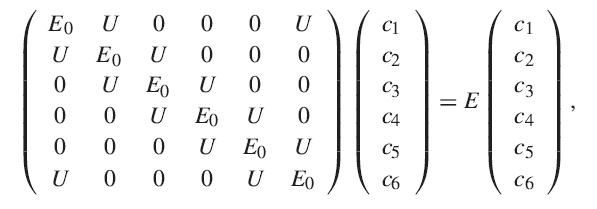

where |ψ〉 = c₁|ψ1〉 + c₂|ψ₂〉 + c₃|ψ₃〉 + c₄|ψ₄〉 + c₅|ψ₅〉 + c₆|ψ₆〉. For convenience, we assume the coupling term U is real. In one dimension, the formulas for the boundary conditions take a simple form: We have b = 2π/a, and k = νb/N = 2πν/Na. Bloch’s theorem tells us that the phase factor from one cell to the next will be e^−ika, which is e^i2πν/N. Show that the solution c_n+1 = e^2πνi/6cn is an eigenvector of the above matrix, for ν = 1, . . . , 6. (It is easy to do this in Mathematica.)

Note that if two eigenvalues are degenerate, then the eigenstates corresponding to these eigenvalues are not unique, and can be written as any linear superposition of the two states with the same eigenvalue. In the above solution, there are two sets of degenerate eigenstates corresponding to k traveling in opposite directions. (Since, in the reduced zone, we would take ν from −3 to 3 instead of from 1 to 6.) One could therefore instead equally well write the coefficients as 2 cos ka = e^ika+e^−ika, 2i sin ka = e^ika − e^−ika. Which eigenvectors does Mathematica give, if you use its eigenvector solver?

Suppose that instead of a ring, we have a chain of six atoms with the ends unconnected. How should you alter the above matrix to describe this system? For a specific choice of E₀ and U, namely E₀ = 1 and U = 0.1, solve for the eigenvalues of both the ring and the linear chain. How much do the eigenvalues differ in the two cases?

Transcribed Image Text:

Eo U U Eo U 0 U Eo 0 0 U Eo 0 0 0 U Eo U 000 U Eo 0 0 0 U 0 U 00 U 0 0 0 U C2 C3 C3 10-4 = E C4 C4 C5 C5 C6 C6