Consider the following FA:

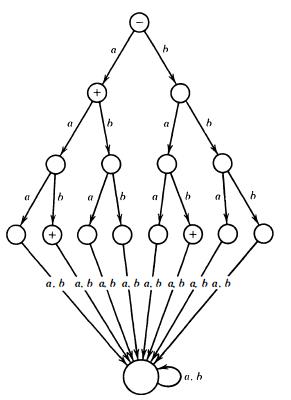
(i) Show that any input string with more than three letters is not accepted by this FA.
(ii) Show that the only words accepted are a, aab, and bab.
(iii) Show that by changing the location of + signs alone, we can make th is FA accept the language {bb aba bba} .
(iv) Show that any language in which the words have fewer than four letters can be accepted by a machine that looks like this one with the + signs in different places.
(v) Prove that if L is a finite language, then there is some FA that accepts l extending the binary-tree part of this machine several more layers if necessary.

h b a b a b a. b a.babababababa.h a. h b