Generate 100 observations in a random walk process starting at \(x_{0}=10\) with a drift term of \(\delta=2\).

Use a white noise process with variance 16, as in Figure 5.2, but distributed as a multiple of a \(t\) random variable with \(4 \mathrm{df}\). 

(a) Plot the observations and fit a least squares trend line. Generate the observations efficiently.

(b) Detrend the data in the random walk with drift by subtracting the fitted values on the trend line, and plot the observations that result.

(c) Now detrend the data in the random walk with drift by use of the difference operator, and plot the observations that result.

(d) At this point, you have three series. Use the KPSS test to assess whether each has a linear trend.

Figure 5.2:

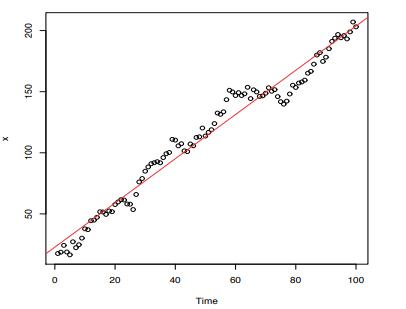
x 50 50 100 150 200 8 20 40 Time 60 80 100