Suppose that \(z_{t}\) is a \(k\)-dimensional weakly stationary, zero-mean time series following the \(\operatorname{VARMA}(2, q)\) model

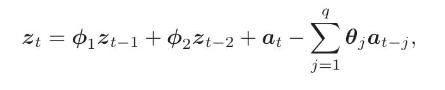
where \(\left\{\boldsymbol{a}_{t}\right\}\) is a white noise series with positive-definite covariance matrix \(\boldsymbol{\Sigma}_{a}\). Let \(\Gamma_{j}\) be the lag- \(j\) autocovariance matrix of \(\boldsymbol{z}_{t}\).

(a) Consider the VAR(2) fitting \[ \boldsymbol{z}_{t}=\boldsymbol{\phi}_{1}^{(0)} \boldsymbol{z}_{t-1}+\boldsymbol{\phi}_{2}^{(0)} \boldsymbol{z}_{t-2}+\boldsymbol{a}_{t}^{(0)} \]
Show that the ordinary LS estimates of \(\phi_{i}^{(0)}(i=1,2)\) satisfy the system of equations

\[ \left[\boldsymbol{\Gamma}_{1}, \boldsymbol{\Gamma}_{2}\right]=\left[\phi_{1}^{(0)}, \phi_{2}^{(0)}\right]\left[\begin{array}{ll} \boldsymbol{\Gamma}_{0} & \boldsymbol{\Gamma}_{1} \\ \boldsymbol{\Gamma}_{1}^{\prime} & \boldsymbol{\Gamma}_{0} \end{array}\right] \]

(b) Let \(\boldsymbol{a}_{t}^{(0)}\) be the residual of the fitted VAR(2) model via the ordinary LS method. Discuss the properties of the autocovariance matrices of \(\boldsymbol{a}_{t}^{(0)}\) when \(q=0\) and when \(q=1\).

(c) Consider the model \[ \boldsymbol{z}_{t}=\boldsymbol{\phi}_{1}^{(1)} \boldsymbol{z}_{t-1}+\boldsymbol{\phi}_{2}^{(1)} \boldsymbol{z}_{t-1}+\gamma_{1}^{(1)} \boldsymbol{a}_{t-1}^{(0)}+\boldsymbol{a}_{t}^{(1)} \]
Show that the ordinary LS estimates of \(\phi_{i}^{(1)}\) satisfy the system of equations \[ \left[\boldsymbol{\Gamma}_{2}, \boldsymbol{\Gamma}_{3}\right]=\left[\phi_{1}^{(1)}, \phi_{2}^{(1)}\right]\left[\begin{array}{ll} \boldsymbol{\Gamma}_{1} & \boldsymbol{\Gamma}_{2} \\ \boldsymbol{\Gamma}_{0} & \boldsymbol{\Gamma}_{1} \end{array}\right] \]

(d) Let \(\boldsymbol{a}_{t}^{(1)}\) be the residual of the LS fit of the model in part (c). Discuss the properties of the autocovariance matrices of \(\boldsymbol{a}_{t}^{(1)}\) when \(q=0,1\), and 2 .

Transcribed Image Text:

t = t1 + $2t2+ at-ja-j j=1