In the Young's interference experiment shown in Fig. 5-5-9pp, the normalized power spectral density \(\widehat{\mathcal{G}}(v)\) of the light is measured at point \(Q\) by a spectrometer. The mutual coherence function of the light is known to be separable,

\[ \boldsymbol{\Gamma}\left(P_{1}, P_{2}, \tau\right)=\boldsymbol{\mu}\left(P_{1}, P_{2}\right) \boldsymbol{\Gamma}(\tau) \]

Show that under the condition \(\left(r_{2}-r_{1}\right) / c \gg \tau_{c}\), when no interference fringes are observed, and assuming that the intensities of the light from pinholes \(P_{1}\) and

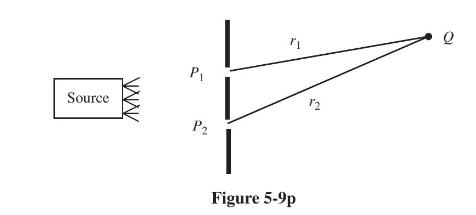
\(P_{2}\) at point \(Q\) are the same, show that \(\boldsymbol{\mu}\left(P_{1}, P_{2}\right)\) can be measured by examining fringes that exist in the normalized spectrum \(\widehat{\mathcal{G}}_{Q}(v)\) of the light at \(Q\). Specify how both the modulus and the phase of \(\boldsymbol{\mu}\left(P_{1}, P_{2}\right)\) can be determined.

Source P 12 P2 Figure 5-9p Q