A general rule states that for independent observations, the variance of yi is the sum of the

A general rule states that for independent observations, the variance of Σyi is the sum of the variances, which is nσ2 for n observations.

(a) Explain intuitively why Σyi would have a larger variance than a single observation y.

(b) Since the variance of a probability distribution is σ2 = E(y − μ)2, explain why the variance of the sampling distribution of ¯y is

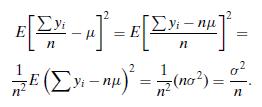
(Hint: The second expression represents a sum with n2 in the denominator, which is a constant that can be put in front of the summation.)

(c) From (b), explain why the standard error equals σ¯y = σ/√n.

Transcribed Image Text:

n n ( Eyi-nu 1 n (no)= n n