Hooke’s Law states that the force F exerted by a spring on a mass is proportional to the displacement from its resting position.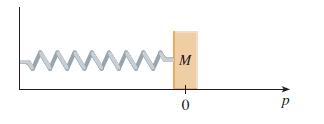

From the figure we have F − 2kp for some positive constant k, where p is position. Also, Newton’s Second Law tells us that F − ma, where m is the mass of the object and a is its acceleration. Further, since we know that acceleration is the second derivative of position with respect to time, we obtain the differential equation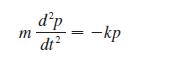

This is a second-order differential equation because it involves the second derivative of the unknown function, p.

(a) Define a new variable q − dpydt. Show that the second-order differential equation can then be written as the following system of two first-order differential equations dp dt − q dq dt − 2 kp m

(b) Construct the phase plane for the equations in part (a), including nullclines, the equilibrium, and the direction of movement.

(c) What does the phase plane analysis from part

(b) tell you about the position of the mass over time?

(d) What does the phase plane analysis from part

(b) tell you about the velocity of the mass over time?

Transcribed Image Text:

www.M www. + 0 P