Radioactive mass 1 emits particles at a mean rate of λ₁per second, and radioactive mass 2 emits particles at a mean rate of λ₂per second. Mass 1 is selected with probability p, and mass 2 is selected with probability 1 ˆ’ p. Let X be the time at which the first particle is emitted. It can be shown that X has a mixed exponential distribution with probability density function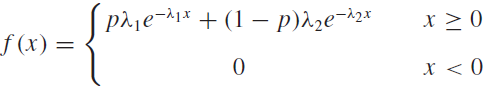

a. Find μ_X.

b. Find the cumulative distribution function of X.

c. Let λ₁ = 2, λ₂ = 1, and p = 0.5. Find P(X ‰¤ 2).

d. Let λ₁ = 2, λ₂ = 1, and p = 0.5. Given that.

P(X ‰¤ 2), find the probability that mass 1 was selected.

|a + (1 )2e-r f (x) = > 0