Extreme value distributions are used to model values of a continuous random variable that represent extremely rare events. For example, an oceanic engineer may want to model the size of a freak wave from a tsunami, or an environmental engineer might want to model the probability of the hottest temperature exceeding a certain threshold. The journal Extremes (March, 2013) investigated several probability distributions for extreme values.

a. The cumulative distribution function for a Type I extreme value distribution with mean 0 and variance 1 takes the form: 

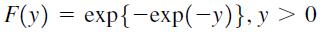
(This is known as the Gumbel distribution.) Show that the property, F(∞) = 1 is satisfied.

b. Refer to part a. Find F(2) and interpret the result.

c. The cumulative distribution function for a Type II extreme value distribution with mean 0 and variance 1 takes the form:

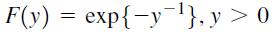
 (This is known as the Frechet distribution.) Show that the property, F(∞) = 1 is satisfied.)

d. Refer to part c. Find F(2) and interpret the result.

e. For which extreme value distribution, Type I or Type II, is it more likely that the extreme value exceeds 2?

Transcribed Image Text:

F(y) %3D еxp{-exp(-у)}. у > 0