In a classic research paper, Hamilton (1987) illustrated the multicollinearity problem with an example using the data shown in the next table. The values of x1, x2, and y in the table represent appraised land value, appraised improvements value, and sale price, respectively, of a randomly selected residential property. (All measurements are in thousands of dollars.)

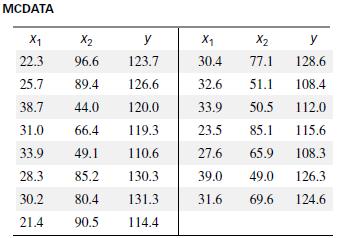
a. Calculate the coefficient of correlation between y and x₁. Is there evidence of a linear relationship between sale price and appraised land value?

b. Calculate the coefficient of correlation between y and x₂. Is there evidence of a linear relationship between sale price and appraised improvements?

c. Based on the results in parts a and b, do you think the model E(y) = β_o + β₁x₁ + β₂x₂ will be useful for predicting sale price?
E1y2 = b0 + b1x1

d. Fit the model in part c, and conduct a test of model adequacy. In particular, note the value of R². Does the result agree with your answer to part c?

e. Calculate the coefficient of correlation between x₁ and x₂. What does the result imply?

f. Many researchers avoid the problems of multicollinearity by always omitting all but one of the “redundant” variables from the model. Would you recommend this strategy for this example? Explain. 

Transcribed Image Text:

MCDATA X1 X2 y X1 X2 y 22.3 96.6 123.7 30.4 77.1 128.6 25.7 89.4 126.6 32.6 51.1 108.4 38.7 44.0 120.0 33.9 50.5 112.0 31.0 66.4 119.3 23.5 85.1 115.6 33.9 49.1 110.6 27.6 65.9 108.3 28.3 85.2 130.3 39.0 49.0 126.3 30.2 80.4 131.3 31.6 69.6 124.6 21.4 90.5 114.4