Let y 1 , y 2 , y 3 be a random sample from an exponential distribution with mean , i.e., E (y i )

Let y₁, y₂, y₃ be a random sample from an exponential distribution with mean θ, i.e., E (y_i) = θ, i = 1, 2, 3. Consider three estimators of θ:

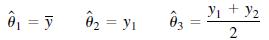
a. Show that all three estimators are unbiased. 

b. Which of the estimators has the smallest variance? Recall that, for an exponential distribution, V(y_i) = θ².

y1 + y2 02 = y %3D 2