Refer to Exercise 14.43. Since charging time is a quantitative factor, we could plot the strength y

Question:

Refer to Exercise 14.43. Since charging time is a quantitative factor, we could plot the strength y versus charging time x1 for each of the four combinations of alloy type and material condition. This suggests that a prediction equation relating mean strength E(y) to charging time x1 may be useful.
Consider the model

E( y) = β₀ + β₁x₁ + β₂x₁² + β₃x₂ + β₄x₃ + β₅x₂x₃ + β₆x₁x₂ + β₇x₁x₃ + β₈x₁x₂ x₃ + β₉x₁²x₂ + β₁₀x₁²x₃ + β₁₁x₁²x₂x₃

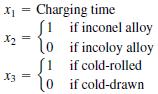
a. Using this model, give the relationship between mean strength E(y) and charging time x₁ for cold-drawn incoloy alloy.

b. Using this model, give the relationship between mean strength E(y) and charging time x₁ for cold-drawn inconel alloy.

c. Using this model, give the relationship between mean strength E(y) and charging time x₁ for cold-rolled inconel alloy.

d. Fit the model to the data and find the prediction equation.

e. Refer to part d. Find the prediction equations for each of the four combinations of alloy type and material condition.

f. Refer to part d. Plot the data points for each of the four combinations of alloy type and material condition. Graph the respective prediction equations.

Data from Exercise 14.43

In increasingly severe oil well environments, oil producers are interested in high-strength nickel alloys that are corrosion-resistant. Since nickel alloys are especially susceptible to hydrogen embrittlement, an experiment was conducted to compare the yield strengths of nickel alloy tensile specimens cathodically charged in a 4% sulfuric acid solution saturated with carbon disulfide, a hydrogen recombination poison. Two alloys were combined: inconel alloy (75% nickel composition) and incoloy (30% nickel composition). The alloys were tested under two material conditions (cold-rolled and cold-drawn), each at three different charging times (0, 25, and 50 days). Thus, 2 × 2 × 3 a factorial experiment was conducted, with alloy type at two levels, material condition at two levels, and charging time at three levels. Two hydrogen-charged tensile specimens were prepared for each of the 2 × 2 × 3 = 12 factor–level combinations.