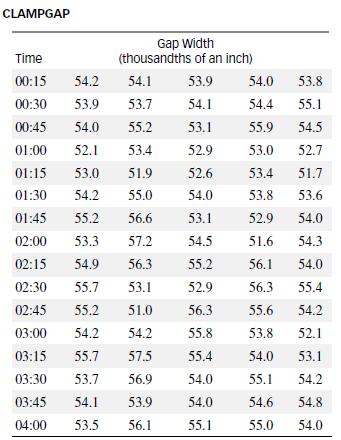
University of Waterloo (Canada) statistician S. H. Steiner applied control chart methodology to the manufacturing of a horseshoe-shaped metal fastener called a robotics clamp (Applied Statistics, Vol. 47, 1998). Users of the clamp were concerned with the width of the gap between the two ends of the fastener. Their preferred target width is .054 inches. An optical measuring device was used to measure the gap width of the fastener during the manufacturing process. The manufacturer sampled five finished clamps every 15 minutes throughout its 16-hour daily production schedule and optically measured the gap. Data for 4 consecutive hours of production are presented in the table.

a. Use all the sample information to find a 95% tolerance interval for 99% of all the gap widths. Assume the distribution of gap widths is approximately normal.

b. Specifications require the gap width of a clamp to fall within 54 ± 4 thousandths of an inch. Based on the “natural” tolerance limits of the process (i.e., the tolerance limits of part a), does it appear that the specifications are being met?

c. How large a sample is required to construct a nonparametric 95% tolerance interval for at least 95% of the gap widths? If n is large enough for this case, give the nonparametric tolerance limits.

Transcribed Image Text:

CLAMPGAP Gap Width (thousandths of an inch) Time 00:15 54.2 54.1 53.9 54.0 53.8 00:30 53.9 53.7 54.1 54.4 55.1 00:45 54.0 55.2 53.1 55.9 54.5 01:00 52.1 53.4 52.9 53.0 52.7 01:15 53.0 51.9 52.6 53.4 51.7 01:30 54.2 55.0 54.0 53.8 53.6 01:45 55.2 56.6 53.1 52.9 54.0 02:00 53.3 57.2 54.5 51.6 54.3 02:15 54.9 56.3 55.2 56.1 54.0 02:30 55.7 53.1 52.9 56.3 55.4 02:45 55.2 51.0 56.3 55.6 54.2 03:00 54.2 54.2 55.8 53.8 52.1 03:15 55.7 57.5 55.4 54.0 53.1 03:30 53.7 56.9 54.0 55.1 54.2 03:45 54.1 53.9 54.0 54.6 54.8 04:00 53.5 56.1 55.1 55.0 54.0