The initial temperature of a certain container is measured to be (T_{0}=20^{circ} mathrm{C}). The ambient temperature is
Question:
The initial temperature of a certain container is measured to be \(T_{0}=20^{\circ} \mathrm{C}\). The ambient temperature is measured to be \(T_{a}=4^{\circ} \mathrm{C}\). An engineer uses Newton's law of cooling to compute the time needed to cool the container to a temperature of \(10^{\circ} \mathrm{C}\). Taking into account the physical properties of the container, this time (in minutes) is computed to be
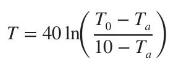
Assume that the temperature measurements \(T_{0}\) and \(T_{a}\) are unbiased and come from normal populations with standard deviation \(0.1^{\circ} \mathrm{C}\).
a. Generate an appropriate simulated sample of values \(T^{*}\). Is it reasonable to assume that \(T\) is normally distributed?
b. Use the simulated sample to estimate the standard deviation of \(T\).
c. If appropriate, use the normal curve to find a 95\% confidence interval for the time needed to cool the container to a temperature of \(10^{\circ} \mathrm{C}\).
Step by Step Answer:






