Max the Bookie is trying to decide how many telephones to install in his new bookmaking operation. Because of heavy police activity, he cannot increase or decrease the number of telephones once he sets up his operation. He has narrowed the possible choices to three. He can install 25, 50, or 100 telephones. His profit for 1 year (the usual length of time he can remain in business before the police close him down) depends on the average number of calls he receives. The number of calls is Poisson distributed. After some deliberation, he concludes that the average number of calls per minute can be .5, 1.0, or 1.5, with probabilities of .50, .25, and .25, respectively. Max then produces the payoffs given in the accompanying table.

Payoff Table

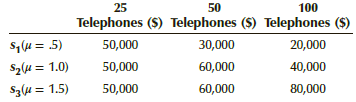
Max€™s assistant, Lefty (who attended a business school for 2 years), points out that Max may be able to get more information by observing a competitor€™s similar operation. However, he will be able to watch for only 10 minutes, and doing so will cost him $4,000. Max determines that if he counts fewer than 8 calls, that would be a low number; at least 8 but fewer than 17 would be a medium number; and at least 17 would be a large number of calls. Max also decides that, if the experiment is run, he will record only whether there is a small, medium, or large number of calls. Help Max by performing a preposterior analysis to determine whether the sample should be taken. Conclude by specifying clearly what the optimal strategy is.

Transcribed Image Text:

25 100 50 Telephones ($) Telephones ($) Telephones ($) 30,000 60,000 60,000 s,(4 = .5) S2(4 = 1.0) S3(4 = 1.5) 20,000 40,000 80,000 50,000 50,000 50,000