An automobile dealership sells two types of four-door sedans, the "Land Yacht" and the "Mini-Rover." The number of Land Yachts and Mini-Rovers sold on any given day varies, with the probabilities of the various possible sales outcomes given by the following table:

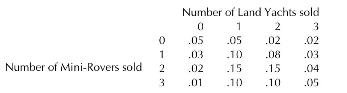 Land Yachts sell for \$22,000 each, and Mini-Rovers for \(\$ 7,500\) each. These cars cost the dealership \(\$ 20,000\) and \(\$ 6,500\), respectively, which must be paid to the car manufacturer.

(a) Define a random variable that represents daily profit above dealer car cost, i.e., total dollar sales-total car cost. (Let \(x=\) number of Land Yachts sold and \(y=\) number of Mini-Rovers sold). What is the expected value of daily profit above dealer car cost?

(b) The daily cost (other than the cost of cars) of running the dealership is equal to \(\$ 4,000\). What is the probability that total profit on a given day will be positive?

(c) What is the expected number of Mini-Rovers sold on a day when no Land Yachts will be sold? What is this expected number on a day when two Land Yachts are sold? Are \(X\) and \(Y\) independent random variables? Why or why not?

Transcribed Image Text:

Number of Mini-Rovers sold 0123 Number of Land Yachts sold 0 2 .05 .03 .02 .01 1 .05 .02 .10 .08 .15 .15 .10) .10 3 .02 .03 .04 .05