SUPERCOMP, a retail computer store, sells personal computers and printers. The number of computers and printers sold on any given day varies, with the probabilities of the various possible sales outcomes being given by the following table:

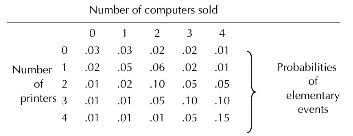
a. If SUPERCOMP has a profit margin (product sales price - product unit cost) of \(\$ 100\) per computer sold and \(\$ 50\) per printer sold, define a random variable representing aggregate profit margin from the sale of computers and printers on a given day. What is the range of this random variable?

b. Define a discrete density function appropriate for use in calculating probabilities of all events concerning aggregate profit margin outcomes on a given day.

c. What is the probability that the aggregate profit margin is \(\geq \$ 300\) on a given day?

d. The daily variable cost of running the store is \(\$ 200 /\) day. What is the probability that SUPERCOMP's aggregate profit margin on computer and printer sales will equal or exceed variable costs on a given day?

e. Assuming that events involving the number of computers and printers sold are independent from day to day, what is the probability that for any given 6-day business week, aggregate profit margins equal or exceed variable cost all 6 days?

Transcribed Image Text:

Number of computers sold 0 1 2 3 4 0 .03 .03 .02 .02 .01 Number 1 .02 .05 .06 .02 .01 of 2 .01 .02 .10 .05 .05 printers 3 .01 .01 05 10 10. 4 .01 .01 .01 .03 15 Probabilities of elementary events