The ultimate moment capacity, M, of an under-reinforced concrete rectangular section is given by

where

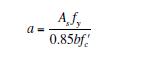
in which the following are random variables: As is the cross-sectional area of the reinforcing steel, fy is the yield stress (strength) of the steel, d is the distance from the reinforcing steel to the top fibers of the beam, b is the width of the beam, and f ???? c is the ultimate stress (strength) of the concrete. Assume that the random variables are statistically noncorrelated with the following characteristics:
Random Variable Mean Value COV Distribution Type F = fy As 40,000 lb 0.15 Lognormal d 15 in. 0.05 Lognormal b 12 in. 0.05 Normal f ′c 3000 psi 0.20 Lognormal The applied random moment has a COV of 0.2 and lognormal distribution type. Using simulation methods, determine the mean value of the applied moment that results in a failure probability of about 0.001 and a COV of the estimated failure probability of, at the most, 0.05.

Transcribed Image Text:

M = A, f, (d) 2