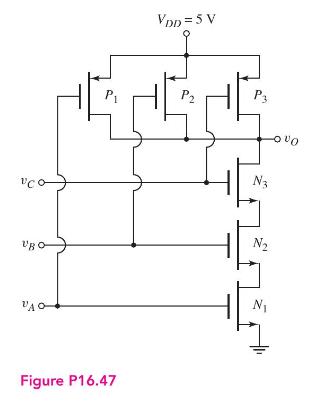
Consider the three-input CMOS NAND circuit in Figure P16.47. Assume (k_{n}^{prime}=2 k_{p}^{prime}) and (V_{T N}=left|V_{T P} ight|=0.8

Consider the three-input CMOS NAND circuit in Figure P16.47. Assume \(k_{n}^{\prime}=2 k_{p}^{\prime}\) and \(V_{T N}=\left|V_{T P}\right|=0.8 \mathrm{~V}\).

(a) If \(v_{A}=v_{B}=5 \mathrm{~V}\), determine \(v_{C}\) such that both \(N_{3}\) and \(P_{3}\) are biased in the saturation region when \((W / L)_{p}=\) \(2(W / L)_{n}\). (State any assumptions you make.)

(b) If \(v_{A}=v_{B}=v_{C}=v_{I}\), determine the relationship between \((W / L)_{p}\) and \((W / L)_{n}\) such that \(v_{I}=2.5 \mathrm{~V}\) when all transistors are biased in the saturation region.

(c) Using the results of part (b) and assuming \(v_{A}=v_{B}=5 \mathrm{~V}\), determine \(v_{C}\) such that both \(N_{3}\) and \(P_{3}\) are biased in the saturation region. (State any assumptions you make.)

Transcribed Image Text:

VAO- Figure P16.47 VDD=5V P2 P3 N3 N N