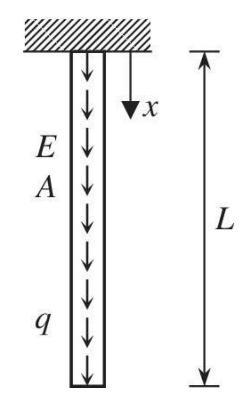
A bar in the figure is under the uniformly distributed load \(q\) due to gravity. For a linear elastic material with Young's modulus \(E\) and uniform crosssectional area \(A\), the governing differential equation can be written as

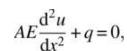
where \(u(x)\) is the downward displacement. The bar is fixed at the top and free at the bottom. Using the Galerkin method and two equallength finite elements, answer the following questions.

a. Starting from the above differential equation, derive an integral equation using the Galerkin method.

b. Write the expression of boundary conditions at \(x=0\) and \(x=L\). Identify whether they are essential or natural boundary conditions.

c. Derive the assembled finite element matrix equation, and solve it after applying boundary conditions.

Transcribed Image Text:

du AE- +q=0, dr