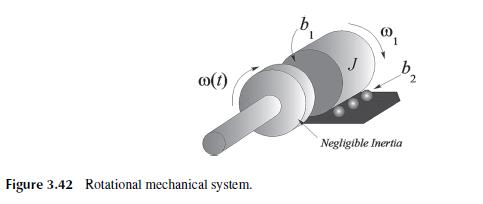
(a) Show that the following rotational mechanical system is represented by the differential equation (Figure 3.42)

\[\dot{\omega}_{1}+\left[\frac{b_{1}+b_{2}}{J}ight] \omega_{1}=\frac{b_{1}}{J} \omega(t)\]

(b) Given the following information: \(\omega(t)=10, b_{1}=b_{2}=1, \omega_{1}(0)=0\) and \(J=2\), find \(\tau\), the time constant and \(\omega_{1_{s s}}\), the steady-state speed.

(c) Deduce the system response (solution to the differential equation).

(d) Solve the same differential equation in (a) with the data in (b) by using Laplace transforms.

(e) Plot the system response and confirm your plot using the IVT and FVT.

Transcribed Image Text:

w(t) 1 Figure 3.42 Rotational mechanical system. Negligible Inertia 2