Analysis of test procedures Let us consider the circuit of Figure 13.20. We want to find, by a path sensitizing approach, one test vector which detect the stuck-at 0 fault of the output of gate D.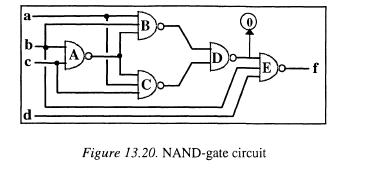

1. The following procedure is proposed:
AllIines are set to 'x' (unknown) state.
f - Input a is set to '0', and a propagation (simulation) is performed towards the fault location: B = 1, C = 1, D = 0, so the fault cannot be activated;
hence we make a backtracking in the input assignment.
Input a is switched to '1', and a propagation is performed that brings nothing, as B and C stay unknown.
Input b is set to '0', and a propagation is performed: B = 1.
Input c is set to '0', and a propagation is performed: C = 1, so the fault cannot be activated; hence we make a backtracking in the input assignment.
Input c is switched to '1', and a propagation is performed: C = 0, D = 0, so the fault is activated as an error e.
Analyze this procedure and complete it in order to find one test vector.
2. The following procedure is proposed:
Alliines are set to 'x' (unknown) state.
- To activate the fault, D is set to 1, and we backtrace this information towards a primary input: one input of gate D must be set to '0'
We choose to set B to '0', and we backtrace this information: all inputs of gate B must be set to '1'.
We choose first the hardiest case, i.e. to assign A to '1', and we backtrace this information.
We chose to set b to '0', and we perform a forward propagation towards the fault of this information: B = 0, so the assignment is inconsistent; we abandon this path and try another one with the assigned values of the primary inputs.

- Gate C is set to '0', this information is backtraced: all inputs of gate C must be set to '1'.
- Input a is set to '1'.
- Input c is set to '1'; now the fault is activated as an error.
- We want to propagate the error through gate E: there is inconsistency.
- We make a backtracking in the primary input assignment.
- Input c is switched to '0', and we perform a propagation: C = 1, so there is inconsistency, and we continue the backtracking on input

b, c being now set to 'x' again.
Complete this procedure in order to find one test vector. Can this procedure be improved?

Transcribed Image Text:

D C B E Figure 13.20. NAND-gate circuit