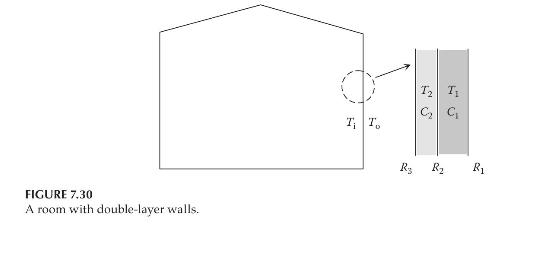
As shown in Figure 7.30, the wall of a room consists of two layers, for which the thermal capacitances are \(C_{1}\) and \(C_{2}\). Assume that the temperatures in both layers are uniform and they are \(T_{1}\) and \(T_{2}\), respectively. The temperatures inside and outside the room are \(T_{\mathrm{i}}\) and \(T_{\mathrm{o}}\), respectively. Both layers exchange heat by convection with air and the thermal resistances are \(R_{1}\) and \(R_{3}\), respectively. The thermal resistance of the interface between the layers is \(R_{2}\).

a. Derive the differential equations for this system.

b. Using the differential equations obtained in Part (a), determine the state-space form of the system. Assume the temperatures \(T_{1}\) and \(T_{2}\) are the outputs.

Transcribed Image Text:

R R1 FIGURE 7.30 A room with double-layer walls. R3