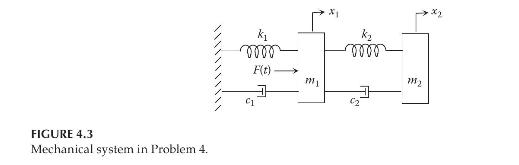
Assuming general initial conditions, express the system model in

a. Configuration form.

b. Standard, second-order matrix form.

\(\left\{\begin{array}{l}m_{1} \ddot{x}_{1}+c_{1} \dot{x}_{1}+k_{1} x_{1}-k_{2}\left(x_{2}-x_{1}\right)-c_{2}\left(\dot{x}_{2}-\dot{x}_{1}\right)=F(t) \\ m_{2} \ddot{x}_{2}+k_{2}\left(x_{2}-x_{1}\right)+c_{2}\left(\dot{x}_{2}-\dot{x}_{1}\right)=0\end{array} ;\right.\) mechanical system in Figure 4.3

Transcribed Image Text:

FIGURE 4.3 Mechanical system in Problem 4. k 0000 F(t) C1 + M 0000 1112