Consider a dynamic system whose plant transfer function and PI controller are given (respectively) by

\[\begin{aligned}G(s) & =\frac{5}{s+1} \\D(s) & =0.1\left(1+\frac{1}{5 s}ight)\end{aligned}\]

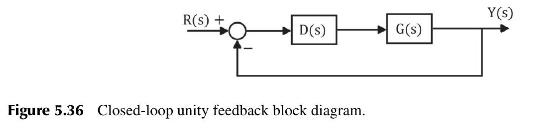
The plant is in a unity feedback arrangement with the PI controller \(D(s)\) as depicted in Figure 5.36.

(a) If the plant is delayed by 3.4 seconds, draw the new block diagram.

(b) Find the exact Transfer Function model of the delayed system.

(c) Using the first-order Pade approximation, find the approximate Transfer Function model of the system.

(d) Hence, determine whether the delayed system is stable.

(e) Use MATLAB to draw the root locus of the delayed system using the exact Transfer Function model (where the Pade approximation is implemented in MATLAB). Then use MATLAB to draw the root locus using the hand-calculated approximate Transfer Function model. Compare the two results.

Transcribed Image Text:

R(s) + Y(s) D(s) G(s) Figure 5.36 Closed-loop unity feedback block diagram.