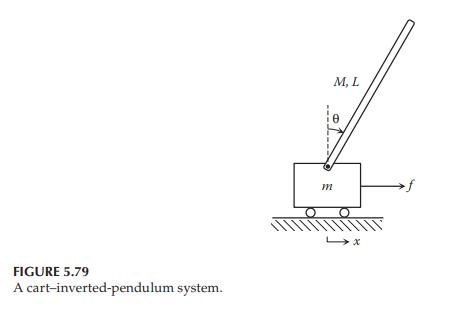
Consider the cart-inverted-pendulum system shown in Figure 5.79. Assume that the mass of the cart is \(0.8 \mathrm{~kg}\), the mass of the pendulum is \(0.2 \mathrm{~kg}\), and the length of the pendulum is \(0.6 \mathrm{~m}\).

a. Determine the poles of the linearized system. Is it stable or unstable?

b. Design a full-state feedback controller for the linearized system using the pole placement method. Assume that two of the closed-loop poles are complex conjugate, with a natural frequency of \(3.6 \mathrm{rad} / \mathrm{s}\) and a damping ratio of 0.6 . They dominate the effect of the other two poles, which are assumed at -10 and -20 .

c. Assume that the initial angle of the inverted pendulum is \(5^{\circ}\) away from the vertical reference line. Using the state feedback gain matrix K obtained in Part (b), examine the responses of the nonlinear and linearized closed-loop systems by using Simulink.

Transcribed Image Text:

FIGURE 5.79 A cart-inverted-pendulum system. m M, L X