Consider the following control system where the feedback gain \(\beta\) is subject to variations.

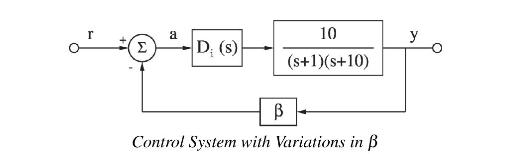
The objective is to design a controller for this system so that the output \(y(t)\) accurately tracks the reference input \(r(t)\).

(a) Let \(\beta=1\), and the following three options for the controller \(D_{i}(s)\) are available:
\[
D_{1}(s)=K, \quad D_{2}(s)=\frac{K}{s}, \quad D_{3}(s)=\frac{K}{s^{2}}
\]
where \(K\) is a constant. Choose the controller (including a particular value for \(K\) ) that will result in a type 1 system with a steady-state error of less than \(\frac{1}{10}\).

(b) Next, suppose that, due to harsh conditions, there is some attenuation in the feedback path modelled by \(\beta=0.9\). Find the steady-state error due to a ramp input for the choice of \(D_{i}(s)\) in part (a).

(c) If \(\beta=0.9\), what is the system type for part (b)?

Transcribed Image Text:

a 10 D; (s) (s+1)(s+10) B Control System with Variations in