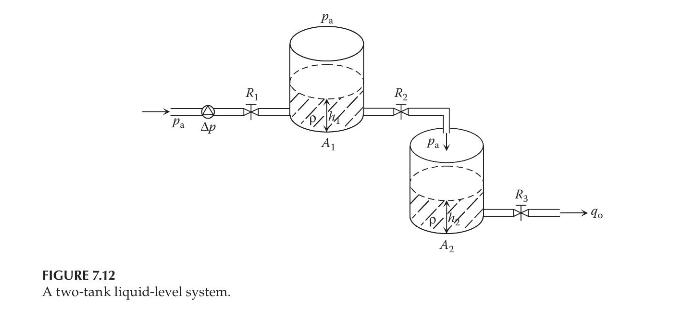
Consider the two-tank liquid-level system in Example 7.5. Construct a Simulink block diagram to find the liquid levels \(h_{1}(t)\) and \(h_{2}(t)\). Assume that \(ho=1000 \mathrm{~kg} / \mathrm{m}^{3}, g=9.81 \mathrm{~m} / \mathrm{s}^{2}\), \(A_{1}=2 \mathrm{~m}^{2}, A_{2}=3 \mathrm{~m}^{2}, R_{1}=R_{2}=R_{3}=400 \mathrm{~N} \cdot \mathrm{s} /\left(\mathrm{kg} \cdot \mathrm{m}^{2}\right)\), and initial liquid heights \(h_{1}(0)=1 \mathrm{~m}\) and \(h_{2}(0)=0 \mathrm{~m}\). The pump pressure \(\Delta p\) is a step function with a magnitude of 0 before \(t=0 \mathrm{~s}\) and a magnitude of \(130 \mathrm{kPa}\) after \(t=0 \mathrm{~s}\).

Data From Example 7.5:

Figure 7.12 shows a liquid-level system in which two tanks have cross-sectional areas \(A_{1}\) and \(A_{2}\), respectively. A pump is connected to the bottom of tank 1 through a valve of linear resistance \(R_{1}\). The liquid flows from tank 1 to tank 2 through a valve of linear resistance \(R_{2}\) and leaves tank 2 through a valve of linear resistance \(R_{3}\). The density \(ho\) of the liquid is constant.

a. Derive the differential equations in terms of the liquid heights \(h_{1}\) and \(h_{2}\). Write the equations in second-order matrix form.

b. Assume the pump pressure \(\Delta p\) as the input and the liquid heights \(h_{1}\) and \(h_{2}\) as the outputs. Determine the state-space form of the system.

Pa Ap FIGURE 7.12 A two-tank liquid-level system. Pa R Pa A R3 90