For designing an automobile suspension, a two-mass system can be used for modelling as shown in the following diagram.

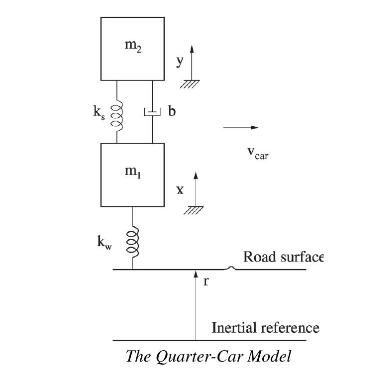
This is called a quarter-car model because it comprises one of the four-wheel suspensions. The car and wheel positions are denoted by \(y(t)\) and \(x(t)\), respectively. These displacements are from static equilibrium, corresponding to no inputs except gravity.

(a) Draw the free-body diagram of this system, assuming one-dimensional vertical motion of the mass above the wheel.

(b) Write down the equations of motion for the automobile.

(c) Express these equations in a State-Variable Matrix model (A, B, C, D) using the following state-variable vector, \[
x(t)=\left[\begin{array}{llll}
x & \dot{x} & y & \dot{y}
\end{array}ight]^{T}
\]
and justify this choice of state variables. Note that the car and wheel positions, \(y(t)\) and \(x(t)\), are the two outputs of the car system while the input is the unit step bump \(r(t)\).

(d) Plot the position of the car and the wheel after the car hits a "unit bump" (i.e. \(r(t)\) is a unit step) using MATLAB. Assume \(m_{1}=10 \mathrm{~kg}, m_{2}=250 \mathrm{~kg}, k_{w}=500,000 \mathrm{~N} / \mathrm{m}, k_{s}=10,000\) \(N / m\). Find the value of \(b\) that you would prefer if you were a passenger in the car.

Transcribed Image Text:

ku ele m eee m X b r y V. car Road surface Inertial reference The Quarter-Car Model