In the following rotational mechanical system, there is a driving torque \(T(t)\) exerted on disk \(J_{1}\) and a load torque \(T_{L}(t)\) exerted on disk \(J_{2}\). Both the applied torque \(T(t)\) and the load torque \(T_{L}(t)\) are considered as inputs and the output is the angular velocity \(\omega_{3}(t)\) (Figure 2.93).

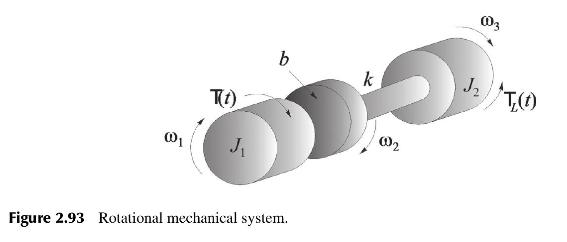
(a) Draw the free-body diagrams for the system.

(b) Explain why the vector of state variables can be chosen as

\[\mathbf{x}(t)=\left[\begin{array}{llll}\theta_{2} & \theta_{3} & \omega_{1} & \omega_{3}\end{array}ight]^{T} .\]

(c) Express the dynamic equations in State-Variable Matrix model (i.e. obtain A, B, C, D).

(b) Use the s-operator method to express the dynamic equations in the form of an input-output differential equation.

Transcribed Image Text:

03 T(t) b k J TA @1 W2 J Figure 2.93 Rotational mechanical system.