Solve the onedimensional heat conduction problem 6 using the RayleighRitz method. For the heat conduction problem, the
Question:
Solve the onedimensional heat conduction problem 6 using the RayleighRitz method. For the heat conduction problem, the total potential can be defined as
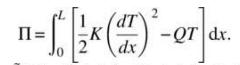
Use the approximate solution \(\tilde{T}(x)=T_{1} \phi_{1}(x)+T_{2} \phi_{2}(x)+T_{3} \phi_{3}(x)\), where the trial functions are given in eq. (2.37) with \(N_{D}=3\) and \(x_{1}=0, x_{2}=L / 2\), and \(x_{3}=L\). Compare the approximate temperature with the exact one by plotting them on a graph.
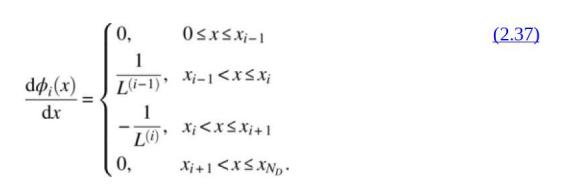
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Finite Element Analysis And Design
ISBN: 9781119078722
2nd Edition
Authors: Nam H. Kim, Bhavani V. Sankar, Ashok V. Kumar
Question Posted:





