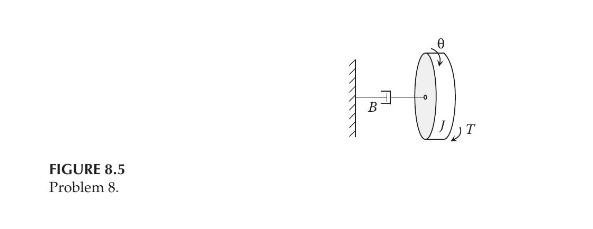
The equation of motion for the torsional mechanical system in Figure 8.5 is derived as \(J \ddot{\theta}+B \dot{\theta}=T(t)\), where \(J, B=\) const, \(\theta\) is the angular displacement, and \(T\) is a constant applied torque. Express the model as first-order in angular velocity \(\omega=\dot{\theta}\). Assuming \(\omega(0)=\omega_{0}\), find \(\omega(t)\). Also identify the transient and steady-state responses.

Transcribed Image Text:

FIGURE 8.5 Problem 8. 1-0 B