The stress matrix at a point (P) is given below. The direction cosines of the normal (mathbf{n})
Question:
The stress matrix at a point \(P\) is given below. The direction cosines of the normal \(\mathbf{n}\) to a plane that passes through \(P\) have the ratio \(n_{x}: n_{y}: n_{z}=3: 4: 12\). Determine:
(a) the traction vector \(\mathbf{T}^{(\mathbf{n})}\);
(b) the magnitude \(T\) of \(\mathbf{T}^{(\mathbf{n})}\);
(c) the normal stress \(\sigma_{n}\);
(d) the shear stress \(\tau_{n}\); and
(e) the angle between \(\mathbf{T}^{(\mathbf{n})}\) and \(\mathbf{n}\). Hint: Use \(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}=1\).
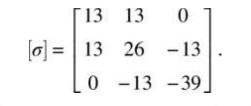
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Finite Element Analysis And Design
ISBN: 9781119078722
2nd Edition
Authors: Nam H. Kim, Bhavani V. Sankar, Ashok V. Kumar
Question Posted:





