Transform the system [begin{aligned}& underline{dot{mathbf{x}}}=mathbf{A} mathbf{x}+mathbf{B u} & mathbf{y}=mathbf{C x}end{aligned}] into observable canonical form, given that the
Question:
Transform the system
\[\begin{aligned}& \underline{\dot{\mathbf{x}}}=\mathbf{A} \mathbf{x}+\mathbf{B u} \\& \mathbf{y}=\mathbf{C x}\end{aligned}\]
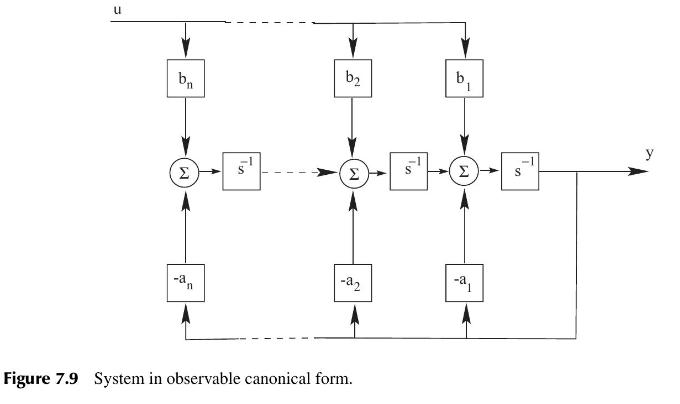
into observable canonical form, given that the system matrices are \[
\mathbf{A}=\left[\begin{array}{lll}
1 & 2 & 2 \\
1 & 4 & 3 \\
3 & 1 & 3 \end{array}ight] \quad \mathbf{B}=\left[\begin{array}{l}
1 \\
0 \\
1 \end{array}ight] \quad \mathbf{C}=\left[\begin{array}{lll}
2 & 1 & 1 \end{array}ight]
\]
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Design And Analysis Of Control Systems Driving The Fourth Industrial Revolution
ISBN: 9781032718804
2nd Edition
Authors: Arthur G O Mutambara
Question Posted:





