Consider a three-phase overhead line made up of three phase conductors: Linnet, (336.4 mathrm{kcmil}), and ACSR 26/7.
Question:
Consider a three-phase overhead line made up of three phase conductors: Linnet, \(336.4 \mathrm{kcmil}\), and ACSR 26/7. The line configuration is such that the horizontal separation between center of \(\mathrm{C}\) and that of \(\mathrm{A}\) is 40", and between that of \(\mathrm{A}\) and \(\mathrm{B}\) is also \(40^{\prime \prime}\) in the same line; the vertical separation of \(\mathrm{A}\) from the line of \(\mathrm{C}-\mathrm{B}\) is \(16^{\prime \prime}\). If the line is operated at \(60 \mathrm{~Hz}\) at a conductor temperature of \(75^{\circ} \mathrm{C}\), determine the inductive reactance per phase in \(\Omega / \mathrm{mi}\),
(a) by using the formula given in Problem 4.14 (a),
(b) by using (4.6.18) from the text.
Problem 4.14
(a) In practice, one deals with the inductive reactance of the line per phase per mile and use the logarithm to the base 10. Show that Eq. (4.5.9) of the text can be rewritten as
\[
\begin{aligned}
x & =k \log \frac{\mathrm{D}}{r^{\prime}} \text { ohms per mile per phase } \\
& =x_{d}+x_{a}
\end{aligned}
\]
where \(x_{d}=k \log \mathrm{D}\) is the inductive reactance spacing factor in ohms per mile \(x_{a}=k \log \frac{1}{r^{\prime}}\) is the inductive reactance at 1 -ft spacing in ohms per mile \(k=4.657 \times 10^{-3} f=0.2794\) at \(60 \mathrm{~Hz}\)
(b) Determine the inductive reactance per mile per phase at \(60 \mathrm{~Hz}\) for a single-phase line with phase separation of \(10 \mathrm{ft}\) and conductor radius of \(0.06677 \mathrm{ft}\). If the spacing is doubled, how does the reactance change?
Eq. (4.5.9)
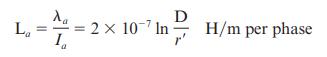
Step by Step Answer:

Power System Analysis And Design
ISBN: 9781305632134
6th Edition
Authors: J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma





