The differential equation of a control system is as follows: Determine the state and output equations of
Question:
The differential equation of a control system is as follows:
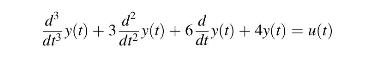
Determine the state and output equations of the system in the matrices form.
1) \(\frac{d}{d t}\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]=\left[\begin{array}{ccc}0 & 1 & 0 \\ 0 & 0 & 1 \\ -4 & -6 & -3\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]+\left[\begin{array}{l}0 \\ 0 \\ 1\end{array}ight] u(t), y(t)=\left[\begin{array}{lll}-1 & 0 & 0\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]\)
2) \(\frac{d}{d t}\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]=\left[\begin{array}{lll}0 & 1 & 0 \\ 0 & 0 & 0 \\ 4 & 6 & 3\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]+\left[\begin{array}{l}0 \\ 0 \\ 1\end{array}ight] u(t), y(t)=\left[\begin{array}{lll}1 & 0 & 0\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]\)
3) \(\frac{d}{d t}\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]=\left[\begin{array}{ccc}0 & 1 & 0 \\ 0 & 0 & 1 \\ -4 & -6 & -3\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]+\left[\begin{array}{l}0 \\ 0 \\ 1\end{array}ight] u(t), y(t)=\left[\begin{array}{lll}1 & 0 & 0\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]\)
4) \(\frac{d}{d t}\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]=\left[\begin{array}{lll}0 & 1 & 0 \\ 0 & 0 & 1 \\ 4 & 6 & 3\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]+\left[\begin{array}{c}0 \\ 0 \\ -1\end{array}ight] u(t), y(t)=\left[\begin{array}{lll}1 & 0 & 0\end{array}ight]\left[\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}ight]\)
Step by Step Answer:

Feedback Control Systems Analysis And Design Practice Problems Methods And Solutions
ISBN: 9783030952761
1st Edition
Authors: Mehdi Rahmani-Andebili





