Life spans of individuals in a population often approximate an exponential distribution, a continuous probability distribution having probability density f(Y)=λe^−λY, where λ is the mortality rate. To estimate the mortality rate of foraging honey bees, Visscher and Dukas (1997) recorded the entire foraging life span of 33 individual worker bees in a local bee population in a natural setting. The 33 life spans (in hours) are listed as follows and in a histogram.

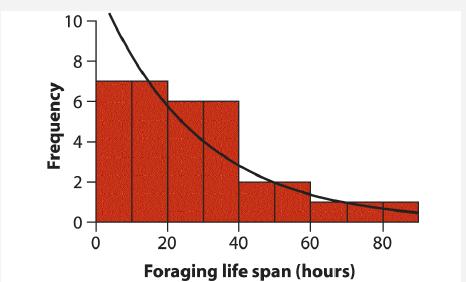
If life span follows an exponential distribution, then the log-likelihood of λ, given the data, is ln L[ λ | observed life spans ]=n ln(λ)−λΣ_iY_i, where Y_i is the life span of individual i, and n is the sample size.

a. Estimate λ, the mortality rate of bees per hour. Using a computer, find the maximum likelihood estimate of λ to two decimal places.

b. What is the value of the log-likelihood at the maximum likelihood estimate λ^{^}?

c. What is the likelihood-based 95% confidence interval for λ?

Transcribed Image Text:

2.3.2.3, 2.3.2.3, 3.9.3.9, 4.0,4.0, 7.1,7.1, 9.5,9.5, 9.6.9.6, 10.8,10.8, 12.8.12.8, 13.6,13.6, 14.6,14.6, 18.2,18.2, 18.2,18.2, 19.0,19.0, 20.9.20.9, 24.3.24.3, 25.8,25.8, 25.9.25.9, 26.5. 26.5, 27.1.27.1, 30.0,30.0, 33.3,33.3, 34.8,34.8, 34.8,34.8, 35.7,35.7, 36.9.36.9, 41.3,41.3, 44.2.44.2, 54.254.2, 55.8.55.8, 65.8,65.8, 71.1.71.1, 84.784.7