Consider a particle moving on the lattice structure depicted in Fig. 6.10. We assume it moves to each of its nearest-neighbour sites with equal probability and that it moves in a way such that within each box it is equally likely to be found at any of the L2i squares, where Li is the linear size of box i, i.e. Li = 2i with i = 1,2,3, . . ..

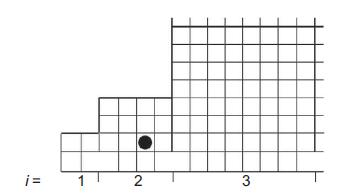
(a) Assume for a moment that the passage between boxes is blocked. What is the entropy of the particle when placed in box i?
Imagine we have an ensemble of systems like the one in Fig. 6.10.We can then think of what on average is happening in this set of equivalent systems. It is natural to estimate the average time between recurrent visits to a given site in box i as given by the inverse of the probability of visiting a site.

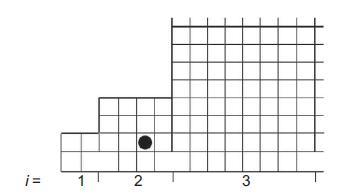
(b) Assume the particle is in box i. What is the probability that the particle is located next to an escape site, see Fig. 6.10?

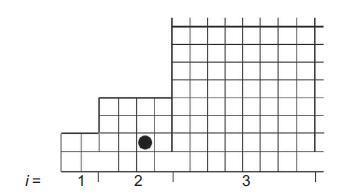(c) What is the probability per time that a particle in box i moves to box i + 1?
(d) What is the probability per time that a particle in box i + 1 moves to box i ?
Now imagine one particle is in box i and one in box i + 1.
(e) Show that the net probability (right move minus left move) for a particle moving from box i to i + 1 is given by 2^−2(i+1).
We see that the particles will move towards higher entropy. Considerations like these were used in [28] to argue about Gaia, evolution and ‘entropic pressure’.

Transcribed Image Text:

= 1 2 3